Выпуклая область на плоскости, часть плоскости, обладающая тем свойством, что соединяющий две её любые точки отрезок содержится в ней целиком (рис.). Любая связная часть границы (см. Связное множество) В. о. называется выпуклой кривой. Примерами таких кривых являются окружность, эллипс, парабола, треугольник, любая дуга окружности, прямая линия, отрезок прямой. Через каждую точку границы В. о. на плоскости проходит по крайней мере одна опорная прямая, имеющая общую точку (или отрезок) с границей области, но не рассекающая последней (на рис. Р, Q, R, S — опорные прямые). В. о. на плоскости могут быть четырёх типов: конечные (граница — замкнутая выпуклая кривая), бесконечные (граница — одна бесконечная кривая; например В. о., ограниченная параболой), бесконечная полоса (граница — пара параллельных прямых), вся плоскость. В. о. может быть задана посредством опорной функции, выражающей расстояние от начала координат до опорной прямой как функцию от внешней нормали к В. о. (т. е. единичного вектора, перпендикулярного опорной прямой и направленного в сторону той из двух полуплоскостей, определяемых этой прямой, в которой нет точек В. о.). В. о. на плоскости представляет собой частный (двумерный) случай n-мepных В. о., которые исследуются в геометрии выпуклых тел.
Э. Г. Позняк.
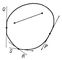
Рисунок к ст. Выпуклая область.