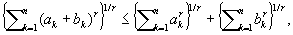
Минковского неравенство, неравенство вида

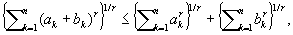
где a_k и b_k (k = 1, 2,..., n) — неотрицательные числа и r > 1. М. н. имеет аналоги для бесконечных рядов и интегралов; оно было установлено Г. Минковским в 1896 и выражает тот факт, что в n-мерном пространстве, для которого расстояние между точками x = (x₁, x₂, ..., x_n) и y = (y₁, y₂, ..., y_n) имеет величину

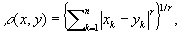
сумма длин двух сторон треугольника больше длины третьей стороны.

Оглавление БСЭ