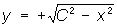 (верхние полуокружности) и
(верхние полуокружности) и 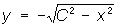 (нижние полуокружности) представляют собой О. р.; соотношение же х2 + y2 = C2 (семейство окружностей) есть общий интеграл (рис.).
(нижние полуокружности) представляют собой О. р.; соотношение же х2 + y2 = C2 (семейство окружностей) есть общий интеграл (рис.).Общее решение обыкновенного дифференциального уравнения
у (n) = f (х, у, у',..., у (n-1)) — семейство функций у= j(x, C1,..., Сп),
непрерывно зависящих от n произвольных постоянных C1,..., Cn, такое, что при соответствующем выборе этих постоянных может быть получено любое решение уравнения (частное решение), однозначно определяемое начальными данными, заполняющими некоторую область n-мерного пространства (см. Дифференциальные уравнения, Коши задача). Если каждая функция у, определяемая соотношением F(x, у, C1,..., Сп) = 0 (и удовлетворяющая соответствующим условиям гладкости), представляет собой О. р. дифференциального уравнения, то такое соотношение называется общим интегралом дифференциального уравнения. Например, для дифференциального уравнения y' = — х/у функции 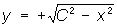 (верхние полуокружности) и
(верхние полуокружности) и 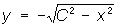 (нижние полуокружности) представляют собой О. р.; соотношение же х2 + y2 = C2 (семейство окружностей) есть общий интеграл (рис.).
(нижние полуокружности) представляют собой О. р.; соотношение же х2 + y2 = C2 (семейство окружностей) есть общий интеграл (рис.).
Аналогично определяется О. р. для системы обыкновенных дифференциальных уравнений.
Лит.: Степанов В. В., Курс дифференциальных уравнений, 8 изд., М., 1959.
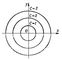
Рис. к ст. Общее решение.