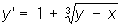О. р. является прямая у = x: через любую точку М0 (х0, у0) этой прямой, кроме самой прямой, проходят интегральные кривые Особое решение дифференциального уравнения, решение, в каждой точке которого нарушается единственность (см. Дифференциальные уравнения). Для уравнения у' = f (x, у) это значит, что через каждую точку О. р. проходит несколько различных интегральных кривых (имеющих в этой точке общую касательную). При непрерывности f (x, у) последнее возможно лишь, если в точках О. р. для функции f (x, у) не выполнено Липшица условие по у. Например, для уравнения 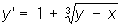О. р. является прямая у = x: через любую точку М0 (х0, у0) этой прямой, кроме самой прямой, проходят интегральные кривые
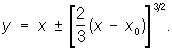
Геометрически О. р. представляет собой огибающую семейства интегральных кривых Ф (х, у, С) = 0, образующих общий интеграл уравнения.
Для дифференциального уравнения F (х, у, у' ) = 0 определяется дискриминантная кривая D (х, у) = 0 как результат исключения параметра р = у' из системы: F (х, у, р) = 0,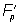 
(х, у, р) = 0. О. р. является, вообще говоря, лишь частью этой кривой.
Лит.: Степанов В.В., Курс дифференциальных уравнений, 8 изд., М., 1959.
Рис. к ст. Особое решение.