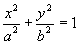Порядок (математический), числовая характеристика математических объектов.

  1) П. алгебраической кривой F (х, у) = 0, где F (х, у) — многочлен от х и y, называют наивысшую степень членов этого многочлена. Например, эллипс 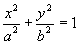 есть кривая второго П., а лемниската (х2 + у2)2 = а2 (х2 — у2) — кривая четвёртого П.

  2) П. бесконечно малой величины a относительно бесконечно малой величины b — такое число n, что существует конечный предел 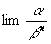 отличный от нуля. Например, sin23х при х ® 0 есть бесконечно малая второго П. относительно х, так как 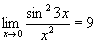. Вообще говорят, что a — бесконечно малая высшего П., чем b, если  и низшего П., чем b, если 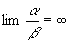. Аналогично определяют П. бесконечно больших величин.

  3) П. нуля (соответственно полюса) а функции f (x) — такое число n, что существует конечный 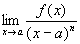 [соответственно lim (х — a) nf (x)], отличный от нуля (см. Нуль функции).

  4) П. производной — число дифференцирований, которые надо произвести над функцией, чтобы получить эту производную (см. Дифференциальное исчисление). Например, у''' — производная третьего П., 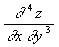 — производная четвёртого П. Аналогично определяют П. дифференциала.

  5) П. дифференциального уравнения — наивысший из П. производных, входящих в уравнение. Например, у’’’ у’ — (y’’)2 = 1 — уравнение третьего П., у’’ — 3у’ + у = 0 — уравнение второго П.

  6) П. квадратной матрицы — число её строк или столбцов.

  7) П. конечной группы — число элементов группы. П. элемента а группы — наименьший положительный показатель n степени an, равной единице группы; если такого n нет, то а называют элементом бесконечного П.

  8) Если при некотором исследовании или вычислении отбрасываются все степени некоторой малой величины, начиная с (n + 1)-й, то говорят, что исследование или вычисление ведётся с точностью до величин n-го П. Например, при исследовании малых колебаний струны пренебрегают величинами, содержащими вторые и высшие степени прогиба и его производных, получая благодаря этому линейное уравнение (линеаризируя задачу).

  9) Слово «П.» употребляется также в исчислении конечных разностей (разности различных П.), в теории многих специальных функций (например, цилиндрические функции n-го П.) и т.д.

  10) При измерениях говорят о величине порядка 10n, подразумевая под этим, что она заключена между 0,5×10n и 5×10n.

 

 

 

Оглавление