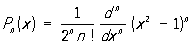Родрига формулы, 1) выражение Лежандра многочленов в виде:

,

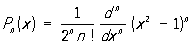данное французским математиком Б. О. Родригом (В. О. Rodrigues) в 1814. Немецкий математик К. Якоби в 1859 обобщил эту формулу на случай Якоби многочленов. В этом случае она имеет вид

.

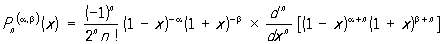  Р. ф. может быть положена в основу теории многочленов Лежандра и Якоби; из неё, в частности, легко выводятся основные свойства этих многочленов. Из неё вытекает также, что многочлены Лежандра и Якоби являются частными случаями гипергеометрической функции.

  2) Выражения для производных единичного вектора нормали m к поверхности в случае, когда параметрической сетью на поверхности является сеть линий кривизны. Если r — радиус-вектор точки М поверхности, R₁ и R₂ — главные радиусы кривизны в точке М, то Р. ф. могут быть записаны следующим образом:

, ,

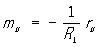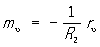(u и u — параметры вдоль линий кривизны). Эти формулы установлены Б. О. Родригом в 1815.

Оглавление