Треугольник прямолинейный, часть плоскости, ограниченная тремя отрезками прямых (стороны Т.), имеющими попарно по одному общему концу (вершины Т.). Т., у которого длины всех сторон равны, называется равносторонним, или правильным (рис., 1), Т. с двумя равными сторонами — равнобедренным (рис., 2). Т. называется остроугольным (рис., 3), если все углы его острые; прямоугольным (рис., 4) — если один из его углов прямой; тупоугольным (рис., 5) — если один из его углов тупой. Более одного прямого или тупого угла Т. иметь не может, так как сумма всех трёх углов равна двум прямым углам (180° или, в радианах, p). Площадь Т. равна ah/2, где а — любая из сторон Т., принимаемая за его основание, a h — соответствующая высота (рис., 6). Стороны Т. подчинены условию: длина каждой из них меньше суммы и больше разности длин двух других сторон. Два Т. конгруэнтны (равны), если они имеют равными (попарно) все стороны или две стороны и угол между ними, или сторону и два прилежащих угла. Числовые соотношения между углами и сторонами Т. изучаются в тригонометрии. О Т. на сфере см. Сферическая геометрия. Сферическая тригонометрия.
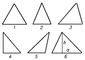
Рис. к ст. Треугольник.