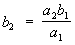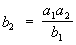Тройное правило, правило для решения арифметических задач, в которых величины связаны прямой или обратной пропорциональной зависимостью (см. Пропорциональность). К задачам на простое Т. п. относятся такие, в которых участвуют две величины x₁ и x₂, причём два значения a₁, a₂ одной из них и одно значение b₁ другой известны. Определению подлежит второе значение величины x₂, то есть b₂. Простое Т. п. основано на пропорциях a₁:b₁ = a₂:b₂ (для прямой пропорциональности) и a₁:b₁ = b₂:a₂ (для обратной пропорциональности), откуда соответственно получаются формулы:

  , .

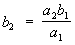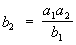  Сложное Т. п. применяется при решении задач, в которых участвуют n (n > 2) величин x₁, x₂,..., x_n-1, x_n. В этом случае у n — 1 величин x₁, x₂,..., x_n-1 известны по два значения a₁, a₂, b₁, b₂,..., l₁, l₂, а у x_n известно только одно значение k₁, другое — k₂ подлежит определению. Практически сложное Т. п. представляет собой последовательное применение простого Т. п.

Оглавление