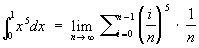Формула (от лат. formula – форма, правило, предписание) (математическая), комбинация математических знаков, выражающая какое-либо предложение; например, суть формулы:

x³ + y³ < z     (1)

2 ´ 2 = 4     (2)

DABC ~ DEFG     (3)

2 ´ 2 = 5     (4)

(a + b)² = a² + 2ab + b²     (5)

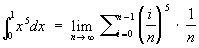,     (6)

y’ = y     (7)

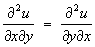     (8)

что с помощью Ф. довольно сложные предложения могут быть записаны в компактной и удобной форме (см. Знаки математические). Некоторые Ф. [из написанных выше (2), (4), (6)] выражают вполне определённые конкретные суждения и поэтому являются истинными [как (2) и (6)] или ложными [как (4)]. Смысл других Ф. [из написанных выше (1), (3), (5), (7), (8)] зависит от значения входящих в них переменных [например, (1) превращается в истинную Ф. 1³ + 2³ < 19 при х = 1, у = 2, z = 19 и в ложную Ф. 3³ + 4³ < 5 при х = 3, у = 4, z = 5]. Ф. этого типа при таком понимании не являются истинными или ложными непосредственно, но становятся таковыми при замещении переменных конкретными объектами из какой-либо заранее выбранной области. Ф., становящиеся истинными при любом замещении переменных объектами из некоторой области, называются тождественно-истинными в данной области. Например, Ф. (5) тождественно-истинна в области комплексных чисел, ф. (8) тождественно-истинна в области дважды непрерывно-дифференцируемых функций от аргументов x и y. Ф., являющиеся истинными [как (2) и (6)] или тождественно-истинными в какой-либо области [как (5) и (8)], служат для записи математических законов. При этом тождественно-истинные Ф. часто понимаются как утверждения о всеобщности. Например, наиболее распространённое понимание Ф. (5) состоит в том, что она считается сокращённой записью следующего утверждения: «для любых чисел а и b имеет место равенство (a + b)² = a² + 2ab + b².

Оглавление