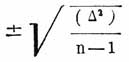
Вероятная ошибка.
— Bсе наши наблюдения и опытные исследования подвержены большим или меньшим ошибкам, причина которых заключается частью в несовершенстве наших чувств, частью в несовершенстве употребляемых нами инструментов. Ошибки эти делятся на постоянные (систематические) и случайные; постоянной ошибкой называется такая, которая при всех измерениях какой-либо величины или остается постоянной, или ее изменения следуют какому-либо определенному закону; случайной же называется ошибка, появляющаяся без определенного порядка и происходящая то в одну, то в другую сторону. Чтобы ослабить влияние случайных ошибок на результат, одни и те же наблюдения повторяют несколько раз, так что для наблюдаемой величины получается несколько болee или менее отличных друг от друга результатов. Наиболее правдоподобным или невероятнейшим значением определяемой величины, если все отдельные наблюдения равно благонадежны, считается среднее арифметическое из отдельных результатов. Разности между средним арифметическим и результатами каждого отдельного наблюдения принимаются за случайные ошибки (при этом предполагается, конечно, что влияние постоянных ошибок уже принято во внимание). Представим себе теперь, что имеется ряд измерений какой-нибудь величины и, следовательно, соответствующий этим измерениям ряд ошибок; та ошибка, численная величина которой такова, что число всех ошибок, меньших ее, равно числу ошибок, больших ее, называется, следуя Гауссу, вероятною (erreur moyenne à craindre); о на дает возможность судить о достоинстве измерения какой-либо величины. Астрономы и геодезисты, измерения которых отличаются чрезвычайною точностью, сообщая результаты своих измерений, приводят обыкновенно и вероятную ошибку их. Вместо вероятной ошибки иногда дается средняя; средней называется такая ошибка, квадрат которой равен среднему арифметическому из квадратов всех ошибок рассматриваемого ряда наблюдений. В простейшем случае, когда для определения искомой величины произведен достаточно многочисленный ряд равно благонадежных измерений, средняя ошибка отдельного измерения вычисляется по формуле
а средняя ошибка результата (среднего арифметического) по формуле
где (Δ 2) означает сумму квадратов всех уклонений отдельных измерений от среднего арифметического, а n — число измерений. Вероятная ошибка приблизительно в полтора раза менее средней. Величину вероятной ошибки можно найти еще следующим, хотя и грубым, способом, вытекающим из самого ее определения: из всего числа ошибок отобрать по порядку половину их, по численной величине наиболее близких к нулю; тогда ошибка, находящаяся на границе отобранных с остальными, и будет приблизительно равна В. ошибке отдельного измерения. В более общем случае, когда различные, не зависимые друг от друга выводы для искомой величины неодинаково благонадежны, при вычислении вероятнейшего значения искомой величины, а также вероятной и средней ошибки ее, принимают в расчет так наз. веса выводов; относительным весом наз. число, обратно пропорциональное квадрату средней ошибки разных выводов, причем единица веса произвольна.
См. Gauss, "Theoria combinationis observationum erroribus minimis obnoxiae" (1821); Буняковский, "Теория вероятностей"; Савич, "Приложение теории вероятностей к вычислению наблюдений etc.".
А. Жданов.