Геометрические сложения и вычитания векторов
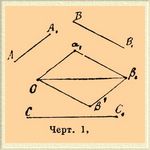
— встречаются весьма часто в физике и механике; таковы, например, сложения сил, приложенных к одной точке, сложения скоростей, ускорений и проч. Геометрическое сложение двух векторов АА 1 и BB1 имеет целью построение третьего вектора СС 1, такого, проекция которого на какое бы то ни было направление равнялась бы сумме проекций на то же направление слагаемых векторов AA1 и ВВ 1. Построение этого вектора CC1, называемого геометрической суммой слагаемых векторов, производится так: из какой-либо точки О (черт. 1) проводится длина О α 1, равная ипараллельная вектору АА 1; из конца её α 1 проводится длина α 1 β 1, равная и параллельная вектору ВВ 1; соединив точку О с β 1, получим длину O β 1, представляющую величину и направление геометрической суммы CC1.
Черт. 1.
Можно сначала отложить O β ', равную и параллельную ВВ 1 и от точки β' отложить β ' β 1, равную и параллельную AA1; — результат получится тот же самый. Можно еще сказать так: геометрическая сумма изображается диагональю параллелограмма, построенного на сторонах равных и параллельных геометрически слагаемым векторам, отложенных от какой-либо точки О, причем и диагональ надо провести из той же точки О. Геометрическое вычитание вектора ВВ 1 из вектора АА 1 имеет целью найти такой вектор DD1 проекция которого на какое-либо направление равнялась бы разности проекций векторов АА 1 и ВВ 1 на то же направление. Говоря иначе, геометрическая разность DD 1 между геометрически уменьшаемым вектором АА 1 и геометрически вычитаемым вектором ВВ 1 равна геометрической сумме векторов AA1 и B1B, причем последний равен и противоположен ВВ 1. Из этого следует, что построение геометрической разности между АА 1 и ВВ 1 должно быть произведено по правилу построения геометрической суммы векторов В 1 В и АА 1, т. е. надо провести O β ' (черт. 2), равную и параллельную В 1 В, из β' провести β ' δ, равную и параллельную АА 1 и соединить О с δ .
Черт. 2.
Если полученную геометрическую разность DD1 геометрически придать к ВВ 1, то их геометрическая сумма будет равна АА 1.
Д. Б.