— в сочинении Архимеда "Об измерении длины окружности" рассматривается вопрос об определении площади и длины окружности круга, а в трактате "О шаре и цилиндре" — о поверхностях и объемах тел, ограниченных кривыми поверхностями; эти вопросы представляют первые геометрические задачи, относящиеся к И. исчислению. И в настоящее время основной задачей И. исчисления является нахождение площадей криволинейных фигур. Под площадью криволинейной фигуры S (черт. 1) разумеется предел, к которому стремится площадь вписанного в фигуру многоугольника по мере увеличения числа его сторон, причем эти стороны могут быть сделаны меньше всякого заранее заданного произвольно малого числа.

Черт. 1.

Указанная задача решается при помощи И. исчисления, если криволинейный контур фигуры S задан уравнением, как это делается в аналитической геометрии (см. Аналитическая геометрия и Дифференциальное исчисление). Пусть уравнение заданной кривой S (черт. 2) есть y = f(x).

Черт. 2.

Определим площадь Р _o М _o М _n Р _n, образованную отрезком оси x -ов P_oP_n, двумя ординатами M_o Р_о и М _n Р _n и дугой М_оМ _n кривой S. Ясно, что нахождение площади всякой криволинейной фигуры может быть сведено к нахождению площадей такого вида (т. е. ограниченным тремя прямыми и дугой кривой). Проведем между крайними ординатами М_о P _о и М _n Р _n п-1 ординат М ₁ Р ₁, М ₂P₂ ..., соответствующих точкам деления Р ₁, Р ₂.... отрезка оси Р _o Р _n. Эти точки выберем произвольно, с тем лишь ограничением, чтобы по мере увеличения числа п наибольший из отрезков был бесконечно мал (напр. точки Р ₁, Р ₂.... можно выбрать на равных расстояниях друг от друга). Предполагая, как это имеет место на черт. 2, что ординаты кривой во все время при переходе от M_o к M_n возрастают, легко видеть, что криволинейная площадь фигуры S будет заключаться между следующими двумя суммами:

S_n = f(x_o)(x₁ — x_o) + f(x₁)(х ₂ — х ₁) +.... + f (x_n-1)(x_n — x_n-1)

и S'_n = f(x₁)(х ₁ — х _o) + f(x₂)(х ₂ — х ₁) +... + f(x_n)(x_n — x_n-1)

где x _о = ОР _o, х ₁ = ОР ₁, x₂ = ОР ₂ ..... x_n = ОР _n

a f(x_o) = M_oP_o, f(x₁) = М ₁ Р ₁, f(x₂) = М ₂P₂....... f (х _n) = М _n Р _n.

Из чертежа очевидно, что

S_n < S < S'_n.

Для обратного случая, т. е. когда ординаты кривой уменьшаются при переходе от M_o к M_n, рассуждение будет то же самое, только последнее неравенство изменит знак, т. е. будет:

S_n > S > S'_n.

Докажем, что разность S'_n — S_n при возрастании числа n может быть сделана как угодно мала. Вычитая на самом деле, имеем:

S'_n — S_n = [f(x₁) — f(x_o)](x₁ — x _о) + [f(x₂) — f(x₁)](x₂ — x₁) +....+ [f(x_n) — f(x_n-1)](x_n — x_n-1).

Вследствие непрерывности функции f(x) в границах рассматриваемой площади число п можно подобрать настолько большим, что все разности f(x₁) — f(x_o), f(x₂) — f(x₁).... f(x_n) — f(x_n-1) выйдут меньше ε, где ε произвольно малое число. Тогда

S' _п — S_n < ε (x₁ — x _о) + ε (x₂ — x₁) + ... + ε (x_n — x_n-1)

т. е. S'_n — S_n < ε (x_n — x_o)

а произведение ε (x_n — x_o) из конечного числа на бесконечно малое ε, очевидно, есть величина бесконечно малая. Отсюда следует, что S можно рассматривать как предел S_n при возрастании п, так что

S = пред. { f(x_o)(x₁ — x_o) + f(x₁)(x₂ — x₁)+ ... + f(x_n-1)(x_n — x_n-1) } при n = ∞.

Введем означения:

x₁ — x_o = Δ x_o, x₂ — x₁ = Δ х ₁ .... х _n — x_n-1 = Δ x_n-1, тогда

S = пред. { f(x_o) Δ x_o + f (x₁) Δ x₁ + .... + f(x_n-1) Δ x_n-1 } при n = ∞

или короче

S = пред. ∑f(x)∙ Δ x.

Этот предел называется определенным интегралом, взятым от f(х) между границам и x_o и x_n; для него употребляют особый знак:

Функция f(x) называется подынтегральной, а значки x₀ и x_n пределами: x _o — нижним, а x_n — верхним пределами. Знак ∫ произошел от буквы S, выражающей сумму элементов f(x)∙dx; название же интеграл произошло от латинского слова integer — целый. Знак ∫ введен Лейбницем и долгое время его употребляли без означения пределов; указание пределов введено Фурье.

Пример. Вычислить площадь 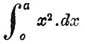, ограниченную осью х-ов (черт. 3) между началом координат и точкой, имеющею абсциссу а, между дугой параболы ОМ, уравнение которой есть у = х ², и ординатой Ma.

Черт. 3.

Разобьем основание Оа на n равных частей a/n = h; тогда площадь ОМа будет пределом суммы

∑ х ² h = оh + h ²h + (2h)²h +... + ((n-1)h)²h = h³(1 + 2² +...+ (n-1)²) = [a³/ n³]∙[(n-1)n(2n-1) /6] или

∑x²h = [a³/3][1 — 3/2n + 1/2n²].

При увеличении n до ∞ получим

пред. ∑ x²h = A³/3

так что

Зная, что aM = a², заключаем, что площадь криволинейной фигуры ОМа равна одной трети площади прямоугольника ОКМа.

Необходимо заметить, что определение интеграла как предела суммы дает возможность вычислить его с любой степенью точности. Для этой цели можно поступать так: разобьем промежуток х _n — x _о (черт. 2) на n равных частей x₁, x₂, x₃, .... х _{n— 1}, х _n; тогда

x₁ = x _о + h, x₂ = x _о + 2h,..... x_n = x _о + nh; отсюда:

S_n = h{f(x_o) + f(x₁) +... + f(x_n-1)}

S'_n = h{f(x₁) + f(x₂) +... + f(x_n)}

Вычитая, получим

S'_n — S_n = h{f(x_n) — f(x_o)}

Подбирая n настолько большим, чтобы h вышло меньше k/[f(x_n) — f(x_o) ], получим

S'_n — S_n < k

и, следовательно, определенный интеграл S будет отличаться от S_n меньше, чем на величину k. Отсюда вычислить интеграл с точностью k значит вычислить соответствующую сумму S_n.

Здесь указана, конечно, только возможность вычисления определенного интеграла с данной степенью точности. В настоящее время в математике известны различные приемы для приближенного вычисления интегралов (площадей), более удобные, чем прием, получаемый непосредственно из определения интеграла как предела суммы. Приемы эти, принадлежащие Симпсону, Котесу, Эйлеру, Гауссу, Чебышеву, Эрмиту и др., известны под названием формул квадратур, откуда название квадратур дается и самим интегралам, так что, если говорят, что вопрос решается в квадратурах, это значит, что искомую величину можно выразить при помощи интегралов от некоторых функций.

Из вышеприведенного примера видно, что вычисление определенного интеграла равносильно задаче вычисления площади некоторого криволинейного контура. Оказывается, что вычисление определенного интеграла от любой функции может быть приведено к одной общей задаче, основной в И. исчислении, а именно к интегрированию функций. Эта задача формулируется так: дана функция f(x); найти новую функцию F (x), называемую первообразной (неопределенный интеграл), так, чтобы F'(x) = f(x), т. е. чтобы заданная функция была производной от искомой. В самом деле, рассмотрим площадь АВРМ (черт. 4), ограниченную отрезком оси х-ов ВР, дугой, заданной кривой AM, ординатой AB некоторой определенной точки А, от которой отсчитываются дуги по кривой AM, и переменной ординатой МР, соответствующей некоторой точке M кривой линии, не указывая, которой именно.

Черт. 4.

Положение переменной ординаты МР, конечно, зависит от абсциссы х = ОР точки М. Поэтому и площадь S = ABPM есть некоторая функция от х; означим ее через F(x). Посмотрим, чему равна производная этой функции. Приращение Δ S = Δ F(x) есть не что иное, как площадь МPР ₁ М ₁, где РР ₁ = Δ x. Если в сопредельности с точкой M функция возрастает, как это имеет место на чертеже, то

PMN₁P₁ < Δ S < РN ₂M₁ Р ₁.

Если бы в сопредельности с точкой M функция убывала, то можно написать такое же неравенство, но с обратным знаком. Вводя предыдущие обозначения и видя, что РМ = f(x), a P₁M₁ = f(x + Δ x), имеем:

f(x) Δ x < Δ F(x) < f(x + Δ x) Δ x.

Разделяя все части этого неравенства на Δ x, получим

f(x) < Δ F(x)/ Δ x < f(x + Δ x);

откуда в пределе:

пред. {Δ F(x)/ Δ x} = F'(x) = f(x).

Итак, нахождение определенных интегралов сводится к поставленной выше задаче. Очевидно, эта задача неопределенная, потому что существует бесчисленное множество функций, имеющих ту же самую производную. Все эти функции отличаются друг от друга на числа постоянные, так как производная от постоянного числа равна нулю. Если, например, обозначить через F(х) одну из бесчисленного множества функций, имеющих производной заданную функцию f(x), то другие функции будут F(x) + 1, F(x) + 2, F(x) + π и т. д., вообще говоря, F(x) + С, где С — некоторое постоянное число, не зависящее от х. Функция F(x) + С, заключающая неопределенную постоянную С, называется поэтому неопределенным интегралом и обозначается так:

∫f(x)∙dx = F(x) + C.

Что в выражение площади должна входить некоторая произвольная постоянная, ясно из геометрических соображений, ибо площади можно отсчитывать от совершенно произвольной ординаты AB (черт. 4). Выбору некоторой ординаты за начальную будет соответствовать аналитическое указание постоянного числа С. Положим, что за начальную ординату счета площадей выбрана ордината, соответствующая некоторому числу а; тогда, если конечную ординату площади означить через х и положить, что х > а, то площадь выразится некоторым числом. По мере приближения ординаты х к начальной а площадь будет уменьшаться, так что при х = а она обратится в нуль. Согласно тому, что уже сказано о пределах определенного интеграла, рассматриваемая площадь может быть обозначена интегралом:

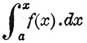
Рассматривая верхний предел х как переменную величину, легко видеть, что этот интеграл равен F(x) + С_о, где С_о подобрано так, что этот интеграл (площадь) обращается в нуль при х = а; отсюда

F(a)+ C_o = 0 и С_о = -F(a);

так что

Этот интеграл назывался Эйлером integrale quod evanescit posito x = a, так как Эйлер не употреблял еще знаков пределов.

Отсюда ясно, что всякий определенный интеграл от функции f (х) между пределами a и b может быть вычислен по формуле

где F(x) совершенно произвольное значение неопределенного интеграла. Это значит, что за F(x) нужно взять совершенно произвольную из числа функций, имеющих заданную производную. Сказанное, впрочем, очевидно, потому что если означить через Ф(х) другое значение неопределенного интеграла, то получается

Ф(х) = F(х) + С;

подставляя вместо x, a и b получим

Ф(a) = F(а) + С Ф(b) = F(b) + С

откуда

Ф(b) — Ф(а) = F(b) — F(а)

и, следовательно, можно взять другое значение неопределенного интеграла Ф(х), так что рассматриваемый определенный интеграл можно вычислить по формуле

Независимость определенного интеграла от той функции из числа первообразных, которую мы выбираем, следует и из того, что площадь между двумя определенными ординатами не зависит от положения третьей ординаты, принятой за начало счета площадей. — И. исчисление разделяется на следующие большие отделы:

I. Интегрирование функций. Здесь излагаются приемы для нахождения по заданной функции ее первообразной, другими словами — нахождение неопределенного интеграла от заданной функции. — Прежде всего необходимо заметить, что знаки дифференцирования и интегрирования друг друга уничтожают, т. е.

d∫f(x)∙dx = f(x)∙dx

и ∫ df(x) = f(x) + C.

Постоянный множитель можно выносить из-под знака интеграла, т. е.

∫a∙f(x)∙dx = a∫f(x)∙dx;

это очевидно как из определения интеграла как предела суммы, так и из понятия о интеграле, как о функции первообразной. Аналогичная теорема существует и в дифференциальном исчислении. В статье Дифференциальное исчисление (см.) помещена табличка производных и дифференциалов простейших функций. Обращение ее дает основную табличку и для интегрирования функций. Возьмем, например, формулу для дифференциала степени:

d(x^a) = a.x^a-1∙dx.

Взяв интегралы обеих частей, или, как говорят, интегрируя обе части этого уравнения, получим:

∫d(x^a) = ∫a∙x^a-1∙dx = a∫x^a-1dx

откуда

x^a + C = a∫x^a-1∙dx

т. е.

∫x^a-1∙dx = x^a/a + С

при заменении а через а + 1 эта же формула представится так:

∫x^a∙dx = x^a+1/(a + 1) + C.

Эта формула не имеет места при а = -1, но тогда на основании формулы (8) упомянутой таблички получим:

∫dx/x = lgx + C

Применяя подобные же рассуждения ко всем прочим формулам таблички дифференциалов простейших функций, получим табличку основных формул интегрирования простейших функций:

1) ∫x^a∙dx = x^a+1/(a + 1) + C

2) ∫dx/x = lgx + C

3) ∫e^xdx = e^x + C

4) ∫a^x∙dx = a^x/lga + C

5) ∫sinx∙dx = -cosx + С

6) ∫cosx∙dx = sin x + С

7) ∫dx/cos²x = tgx + C

8) ∫dx/(1 — x²)^1/2 = arcsinx + C

9) ∫dx/(1 + x²) = arctgx + C

Из этой таблички видно, что интегралы от весьма простых алгебраических функций

∫dx/x, ∫dx/[√(1 — x²)^1/2 ] и ∫ dx/(1 + x²)

выражаются трансцендентными функциями:

lgx, arcsinx и arctg x.

Изыскивая же правила для интегрирования более сложных функций, уже первые исследователи в области И. исчисления заметили, что только интегралы немногих функций вообще представляются в конечном виде; для огромного же большинства функций их первообразные представляют новые виды функций, изучение которых и составляет обширное и еще мало разработанное поле исследований. К числу таких новых трансцендентных принадлежат так называемые эллиптические интегралы, теория которых в настоящее время уже хорошо разработана и получила большие приложения. Интегрирование же функций более сложных состоит пока из отдельных попыток, причем рядом преобразований стремятся свести интегрирование рассматриваемой функции к интегрированию функций, помещенных в табличке простейших. Эта часть И. исчисления доставила, однако, весьма важные результаты; так, например, известно, что интеграл от всякой рациональной функции выражается в конечном виде, т. е. при помощи конечного числа знаков функций, встречающихся уже в элементарной математике. Из числа иррациональных функций заслуживает особенного внимания случай, когда иррациональность подынтегральной функции состоит или из дробных степеней переменного независимого, или же представляет квадратный корень из многочлена, степени не выше второй. В этих случаях интегрирование также совершается в конечном виде. Известны, наконец, некоторые интегрируемые классы функций трансцендентных. К числу упомянутых выше основных преобразований относятся:

1) разложение интеграла на части по формуле:

∫(u + v -w)dx = ∫u∙dx + ∫v∙dx — ∫w∙dx... (I)

2) введение новой переменной, по формулам:

x = φ (t) dx = φ '(t)∙dt... (II)

откуда

∫f(x)dx = ∫f[ φ (t)]∙ φ '(t)∙dt

и 3) интегрирование по частям по формуле:

∫u∙dv = u∙v — ∫v∙du... (III)

II. Теория определенных и кратных интегралов. Сюда относятся исследования и нахождения определенных интегралов в тех случаях, когда неопределенный интеграл весьма трудно или вовсе нельзя выразить через известные функции, а потому тут излагаются приемы, дающие возможность вычислять определенные интегралы не пользуясь основной формулой (*); здесь также обобщается понятие об определенном интеграле на случай нескольких независимых переменных.

III. Геометрические приложения интегрального исчисления. В этом отделе рассматриваются четыре основные задачи: 1) квадратура площадей, ограниченных кривыми линиями, 2) вычисление длин дуг кривых линий, 3) вычисление объемов (кубатура) тел, ограниченных кривыми поверхностями, и 4) вычисление площадей криволинейных поверхностей в некоторых контурах, проведенных на этих поверхностях.

Чтобы дать понятие о геометрических приложениях И. исчисления, а равно о кратных интегралах, рассмотрим задачу об определении объема тел, ограниченных кривыми поверхностями. Такой объем U (черт. 5) можно рассматривать как сумму параллелепипедов, составленных приращениями координат Δ x, Δ у и Δ z, распространенную на все пространство, ограниченное заданной поверхностью.

Черт. 5.

Отсюда общая формула для объема будет:

U = пред. ∑Δ x. Δ у. Δ z

Этот предел обозначается тройным интегралом

U = ∫∫∫dx.dy.dz

который представляет, следовательно, общую формулу для нахождения каких угодно объемов. Вся задача состоит в указании пределов у трех знаков интеграла, так как одно интегрирование (суммирование) производится по букве х, другое по букве у, а третье по букве z. Требуется указать пределы таким образом, чтобы при интегрировании были приняты в расчет все элементы, лежащие внутри рассматриваемого криволинейного тела. Полученная выше формула квадратур ∫ y.dx может быть написана также в виде двойного интеграла ∫ dx.dy, потому что

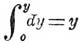
IV. Интегрирование дифференциальных уравнений (см.).

Исторический очерк развития И. исчисления см. Математика. Укажем здесь еще классические сочинения и руководства по этому предмету. Полная система интегрального исчисления в том виде, как оно излагается в настоящее время, находится в знаменитом трактате Эйлера "Institutiones calculi integralis" (СПб., 4 тома). Затем укажем на Коши: "Oeuvres compl è tes", Бертрана: "Trait é de calcul différentiel et de calcul intégral" (2 тома), Ceppe: "Cours de calcul diff érentiel et inté gral" (2 тома), Поссе: "Курс интегрального исчисления" (СПб., 1891 г.), и курсы, указанные в конце статьи Дифференциальное исчисление.

Оглавление