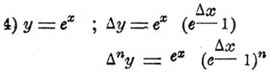
Исчисление конечных разностей
— Конечной разностью функции от одной или нескольких переменных называется приращение функции при данных конечных приращениях переменных независимых. Под И. конечных разностей разумеют совокупность правил: 1) для определения изменений, которым подвергаются функции при конечных приращениях входящих в них переменных, и 2) для определения первообразных функций, когда измененные их виды известны (прямой и обратный способы). При первом появлении дифференциального исчисления приращения переменных величин рассматривались как бесконечно малые величины, вторыми и высшими степенями которых пренебрегали, вследствие чего у многих из математиков явилось сомнение в строгости самого способа и верности результатов, получаемых дифференциальным исчислением. Чтобы доказать справедливость нового способа, английский математик Тейлор, в своем сочинении " Methodus incrementorum directa et inversa", изданном в 1715 году, предложил способ И. конечных разностей, в котором приращения переменных рассматривались как конечные величины, высшими степенями которых уже нельзя пренебрегать. Однако И. конечных разностей, представляющее в сущности И. рядов, имеет, как заметил Лагранж, мало общего с дифференциальным исчислением, предмет которого есть исчисление производных функций. Первые следы И. конечных разностей видны в некоторых приемах Фермата, Баррова и Лейбница, но основателем способа, как самостоятельного исчисления, следует считать Тейлора. Позднейшими за тем исследователями были Николь, Кондорсе, Эмерсон, Эйлер, Лагранж и Лаплас. Они усовершенствовали эту важную отрасль чистого анализа и показали различные ее приложения к интерполированию и суммированию рядов, к теории соединений и в особенности к теории вероятностей.
I. Прямой способ разностей, или собственно И. конечных разностей. Если имеется некоторая функция у = f(х) и для переменной независимой взяты последовательные значения х 1, х 2, х 3.., то у тоже получит последовательные определенные значения у 1, у 2, y3... Разности между двумя последовательными значениями функции, т. е. у 2 — у 1, у 3 — у 2... называются первыми разностями и означаются через Δ у 1, Δ y2... Разности двух последовательных первых разностей называются вторыми разностями данной функции и обозначаются через Δ 2 у и т. д. означая разности последовательных значений х тоже через Δ х 1, Δ х 2 и т. д. выходит
Δ х 1 = х 2 — х 1
Δ х 2 = х 3 — х 2
.......................
.......................
Δ х n—1 = xn — xn—1
Откуда
x2 = x1 + Δ x1
x3 = x1 + Δ x1 + Δ x3
................................
................................
xn = x1 + Δ x1 + Δ x2 + ... + xn — 1,
так что каждое следующее х получается из начального и всех предыдущих разностей. Таким же образом существует закон для получения последовательных значений функций у, именно:
Δ у 1 = у 2 — у 1
Δ у 2 = у 3 — у 2
.....................
.....................
Δ yn — 1 = yn — yn—1 … (1)
Откуда:
у 2 = у 1 + Δ у 1,
у 3 = у 2 + Δ у 2 = у 1 + Δ у 1 + Δ ( у 1 + Δ у 1) = у 1 + 2 Δ у 1 + Δ 2 у 1
у n = у 1 + n Δ y2 + ([n(n — 1)]/2)(Δ 2y1) + ... + Δ nyn
Разности высших порядков будут
Δ 2y1 = Δ y2 — Δ у 1, = у 3 — 2 у 2 + у 1,
Δ 3y1 = Δ 2y2 — Δ 2y1 = y4 — 3 Δ 3 у 3 + 3y2 — у 1,
Δ ny1 = yn — nyn — 1 + ([n(n — 1)]/2)(yn — 1) ... ± y
Таким образом значения у n и Δ n у можно представить символическими формулами:
yn = (1 + Δ y)n и Δ ny = (y — 1)n … (2)
в которых показатели степени следует заменить показателями порядка у и Δ у. Развертывая Δ у в ряд Тейлора и означая производные функции (см. Дифференциальное И.) от у по х через (dy/dx)(d2y/d2x) получим:
Δ y = (dy/dx) Δ x + (d2y/dx2)(Δ x2/2) + ...,
если вместо у последовательно вставлять Δу, то будет:
Δ ny = A(dny/dxn)(Δ xn) + A1(dn+1y/dxn+1)(Δ xn+1) + ...,
Развертывая первую часть в ряд по символической формуле (2) и сравнивая коэффициенты у одинаковых степеней Δ х можно определить коэффициенты А, А 1, …
Приведем табличку конечных разностей некоторых простейших функций:
1) у = xn, Δ y = nxn — 1 Δ x + ([n(n — 1)]/2)(xn — 2 Δ x2) + ... + Δ xn
Δ ny = n(n — 1)(n — 2) ... 1∙ Δ xn
2) у = uv; Δ у = и Δ v + v Δ u + Δ u Δ v
3) y = u/v; Δ y = ex
5) y = lgx; Δ y = lg(1 + Δ x/x)
6) y = Sinx; Δ у = 2Cos(x + Δ x/2)Sin(Δ x/2)
7) y = Cosx; Δ y = —2Sin (x + Δ x/2)Sin(Δ x/2)
II. Обратный способ разностей, или И. конечных сумм.
Если имеется уравнение
Δ y = f(x) … (3),
где f(x) изображает данную, а у неизвестную функцию от переменной x, то определение первообразной функции у приводится к суммированию (интегрированию в конечных разностях) функции f(x). Интеграл в конечных разностях у обозначают греческой Σ, поставленной перед функцией, для которой ищут первообразную, так что
у = Σ f(x)
Покажем, что нахождение первообразной функции у приводится к суммированию. Слагая равенства (1), получаем:
yn = y1 + Δ y1 + Δ y2 + ...+ Δ yn — 1
Положим, что приращение Δ x переменной независимой х постоянное, и обозначим его через h. Кроме того, пусть у 1 соответствует начальному значению x, равному а. Тогда, принимая во внимание уравнение (3) и обозначая у 1 через А, получим
y = A + f(a) + f(a + h) + ... + f[( а + (n — 1)h] … (4).
Если а + nh обозначить через x, то последнее выражение увеличится на
f(а + nh) = f(x),
когда приписать приращение h к последнему значению а + (n — 1)h величины x; следовательно f(x) есть действительно разность второй части, а потому у есть результат суммирования. — Эйлер заметил, что, подобно тому, как в интегральном И., существует бесчисленное множество функций, имеющих заданную производную, причем все эти функции отличаются на постоянные величины, так и в обратном способе разностей, чтобы найти самое общее значение функции, имеющей данную разность, необходимо прибавлять выражение, которое играло бы роль постоянного числа интегрального И., т. е. такое выражение, которое не меняется от прибавления к х постоянного числа h. Этому условию удовлетворяют многие функции, например
Sin(2 π /n) и Cos(2 π /n).
Не излагая правил для суммирования простейших функций, которые имеют большую аналогию с правилами интегрирования функций, приведем здесь простейшие выражения сумм, причем заметим, что конечный интеграл суммы равен сумме интегралов и что постоянный множитель можно выносить из под знака конечной суммы.
На основании этих двух формул можно суммировать любые целые и дробные, рациональные, функции. Мы не будем останавливаться здесь на суммировании иррациональных алгебраических функций, потому что случаи, в которых конечные интегралы выражаются просто, очень редки. Заметим, что, подобно тому, как и в интегральном И., Σ (1/ х) не может быть выражено в алгебраическом виде. Для функций трансцендентных имеются формулы:
Σ ax = ax/ah—1
Σ xmax = axF(xm + Bm—1 ... ) (5)
Σ lg(1 + h/x) = lgx
Σ Sin(a + bx) = — [Cos(a + bx — [bh]/2)]/[2Sin([bh]/2)]
Σ Cos(a + bx) = — [Sin(a + bx — [bh]/2)]/[2Sin([bh]/2)]
Легко заметить, что сумма:
Σ (Ax α + Bx β + ...)Sinmx Cosnx,
если α, β ... m и n числа целые и положительные, приводится к (5) введением мнимостей. Для пояснения вышеприведенных формул применим их к вычислению суммы квадратов и суммы кубов натуральных чисел.
1) Суммируя тождество
x2 = x (х + 1) — x … (а),
имеем
Σ x2 = Σ x(x + 1) — Σ x = [(x — 1)x(x + 1)]/3 — [(x — 1)x]/2
или
Σ x2 = [x(x — 1)(2x — 1)]/6
2) Суммируя тождество
x3 = x(x + 1)(x + 2) — 3x(x + 1) + x … (b),
имеем
Σ x3 = [(x — 1)x(x + 1)(x + 2)]/4 — [(x — 1)x(x + 1)] + [(x — 1)x]/2
или
формула, известная еще китайским математикам. Не нужно забывать, что, согласно уравнению (4), под знаком Σ f(x) разумеются выражения f(1), f(2)... f(x — 1). Что касается тождеств (а) и (b), то их выводят для каждого частного случая, из общих разложений для любой целой функции; приличным выбором постоянных А 0, А 1, ... А n всегда можно удовлетворить тождеству:
По аналогии с дифференциальными уравнениями уравнением в разностях называется всякое уравнение, заключающее переменные величины и их разности. Если обозначим через у искомую функцию от одной переменой x, приращение которой положим постоянной, то общий вид разностного уравнения есть:
F(х, у, Δ у, Δ 2 у ...) = 0.
Вместо разностей Δ у, Δ 2 у ... можно подставить равные им величины у 1 — у, у 2 — 2 у 1 + y ... и тогда предыдущее уравнение обратится в
f ( x, у, у 1, у 2 ...) = 0.
В этом виде обыкновенно и рассматриваются уравнения в разностях. Интегрировать уравнение в конечных разностях значит найти все возможные функции, удовлетворяющие этому уравнению. Методы И. конечных разностей излагаются в курсах дифференциального и интегрального И. Литературу предмета см. соответствующие статьи, а также А. Марков, "И. конечных разностей".
В. Витковский.