Магнетизм
1) Свойства магнитов. Наиболее характерное магнитное явление — притяжение магнитом кусков железа — известно со времен глубокой древности. Однако в Европе вплоть до XII столетия наблюдали это явление лишь с естественными магнитами, т. е. с кусками железной руды, известной ныне под названием магнитного железняка. Самое слово "магнит" (μάγνης, magnes, magnetes) произошло, по всей вероятности, от названия города Магнезия в Лидии, около которого находились большие залежи этой руды. Только в ХII ст. при посредстве арабов проникли в Европу сведения об искусственных стальных магнитах и об их способности повертываться всегда одним своим концом к северу, когда какой-либо из таких магнитов помещается на поплавке, плавающем на поверхности воды (впервые упоминается об этом в сочинении Guyot de Provins, написанном около 1190 г.). Об искусственных стальных магнитах и о пользовании ими при путешествиях по земле и по воде в качестве компасов, т. е. в качестве указателей стран света, знали в Китае уже за 2000 лет до Р. Х. Итак, только в XII ст. стало известно в Европе, что магнит испытывает особое действие Земли. Будучи помещен на поплавке или на острие или будучи подвешен на незакрученной нити, притом так, чтобы была горизонтальна (или близко горизонтальна) прямая линия, соединяющая два места поверхности магнита, в которых наблюдается наиболее сильное притяжение кусков железа, т. е. так называемая магнитная ось магнита, этот магнит принимает вполне определенное положение, если поблизости к нему не имеется масс железа или других каких-либо магнитов. Магнитная ось этого магнита устанавливается в вертикальной плоскости, составляющей некоторый угол (магнитное склонение) с географическим меридианом и называемой магнитным меридианом. Магнит, помещенный на ось, проходящую через центр тяжести его, наклоняется одним своим концом вниз. В северном полушарии опускается вниз северный конец магнита; в южном, наоборот, опускается вниз южный конец магнита. Угол, составляемый при этом магнитной осью магнита с горизонтальной плоскостью, когда плоскость вращения этого магнита совпадает с магнитным меридианом, носит название магнитного наклонения. Помещенный на поплавке, свободно плавающем на воде, магнит вдали от железных масс и других магнитов не испытывает поступательного перемещения. Итак, на магнит действует только направляющая сила, вследствие которой его магнитная ось принимает вполне определенное положение в пространстве. Первый Гильберт выяснил причину этого (в соч. Gilbert, "De magnete magneticisque corporibus et de magno magnete tellura Physiologia nova", 1600). Идея о земном шаре как большом магните, действующем на магниты, находящиеся на земной поверхности, принадлежит Гильберту (см.).
Магниты, находящиеся на расстоянии один от другого, кажущимся образом действуют друг на друга: их одноименные концы взаимно отталкиваются, разноименные — взаимно притягиваются. Кусок железа или стали притягивается магнитом потому, что он сам обращается при этом в магнит. Магнитное состояние этого куска усиливается по мере уменьшения расстояния между ним и магнитом, оно достигает наибольшего развития, когда кусок пристает к тому или другому концу магнита. После отрывания или удаления стали или железа от магнита в них сохраняется магнитное состояние, но далеко не в одинаковой степени в различных сортах этих металлов. В стали остаточный М. получается много сильнее, чем в железе. В мягких сортах железа наблюдаются обыкновенно только следы остаточного М. Совершенно обратное получается во время действия магнита на железо и сталь. Чем мягче железо, тем сильнее в нем возбуждается временное намагничение. Чем тверже сталь — тем слабее этот временной М. Нужно заметить, однако, что ослабление намагничения какого-либо тела после прекращения действия на эти тела намагничивающей силы зависит главным образом от возникновения особой размагничивающей силы, являющейся внутри тела вследствие его намагничения. В очень длинных и тонких проволоках, а также внутри замкнутых колец размагничивающая сила или очень мала (в длинных проволоках), или равна нулю (в замкнутых кольцах). Вследствие этого, как показали опыты Юинга, в тонких и длинных проволоках, а также в замкнутых кольцах, приготовленных из самого мягкого железа, остаточный М. может достигать 97% временного М. (см. Гистерезис). Для приготовления искусственных магнитов употребляются стальные полосы и стержни, прямые и подковообразные. Для сообщения им намагничения или натирают эти полосы и стержни одним концом сильного магнита, при чем конец магнита перемещают вдоль натираемого стержня или полосы всегда в одном направлении, или несколько раз проводят по ним от середины к концам двумя разноименными концами двух магнитов, или помещают их на оба конца сильного электромагнита, или же, наконец, обматывают эти полосы и стержни проволокой и пропускают по проволоке электрический ток (см. Электромагнетизм). Наиболее сильные и наиболее постоянные магниты получаются из вольфрамовой стали, т. е. из стали, которая содержит в себе в виде примеси металл вольфрам. Для этого обыкновенно достаточно 3% вольфрама. Сделанные из такой стали стержни или полосы подвергаются предварительно очень сильной закалке, а затем в течение часов 20 или 30 отпускаются при температуре кипения воды.
Прикосновение железа или стали к короткому магниту, а также натирание последним стальных стержней, т. е. приготовление при посредстве данного магнита других магнитов, почти не производит заметным образом никакого изменения в магнитном состоянии этого магнита. Более точные исследования, однако, обнаруживают некоторые изменения при этом. При приближении железа или стали к магниту несколько изменяется распределение между различными частями поверхности этого магнита способности притягивать железо, т. е. изменяется распределение М. на поверхности магнита. Многократные прикосновения к магниту и отрывания от него железа вызывают заметные ослабления в магнитном состоянии этого магнита. Такое же действие оказывают удары или сотрясения, получаемые магнитом. Наоборот, эти удары и сотрясения, производимые во время намагничения магнита, способствуют намагничению, они усиливают его. Нагревание магнита уменьшает его М. Чем больше это нагревание — тем больше и ослабление магнитного состояния его. Охлаждение магнита до прежней температуры сопровождается восстановлением его магнитного состояния в первоначальном виде только тогда, когда повышение температуры магнита не было очень большое. При температуре, соответствующей оранжевому калению, самая лучшая сталь теряет всякую способность проявлять магнитные свойства. При этой температуре она даже временно не намагничивается под действием самого сильного магнита. Весьма большое охлаждение магнита сопровождается также заметным ослаблением М. этого магнита. Многократные нагревания и охлаждения магнита способствуют большему постоянству магнита. Магнит становится после такого многократного нагревания и охлаждения менее чувствительным к действию теплоты. Самые лучшие стальные магниты не представляются абсолютно постоянными. При полном покое и при отсутствии чувствительных изменений температуры магнитное состояние этих магнитов несколько изменяется с течением времени: магниты становятся слабее. Впрочем, такое ослабление М. в хороших магнитах вообще очень мало и для своего обнаруживания требует особых, весьма тщательных, приемов исследования. Особенно славятся магниты, приготовляемые в Гаарлеме. Логеман был первый, кто доставил своим приготовлением известность гаарлемским магнитам. В след. таблице [Таблица заимствована из соч. С. Томпсона "Электромагнит и электромагнитные механизмы" (переведено с английского М. А. Шателеном, СПб., 1892).] приводятся веса магнитов, имеющих подковообразную форму, и те грузы, которые поддерживаются этими магнитами.
|
Название магнита |
Вес магнита, в кг |
Средняя величина груза, поднимаемого магнитом, в килограммах |
| А |
0,495 |
13,30 |
| В |
0,487 |
11,78 |
| E |
0,889 |
19,02 |
| 3057 |
1,013 |
21,71 |
| 3053 |
1,521 |
27,90 |
| 3054 |
1,918 |
32,53 |
| С |
2,169 |
35,74 |
Ван дер Виллинген дает следующую формулу для вычисления подъемной силы гаарлемских (подковообразных) магнитов:
Здесь Р — подъемная сила в килограммах, S — площадь одной конечной (полюсной) поверхности магнита в квадратных сантиметрах, К — периметр одной конечной (полюсной) поверхности, l — действительная длина подковообразного магнита, L — "уменьшенная" длина его (длина между точками на ветвях магнита, в которых наблюдается наибольший свободный М., иначе наибольшее притяжение железа, когда к магниту приложен якорь. Якорем называется кусок железа с отшлифованной поверхностью, которой он пристает к конечным поверхностям магнита; к этому якорю прикрепляют те грузы, которые должны быть поддерживаемы магнитом). Величины L и l должны быть выражены в сантиметрах. В — коэффициент, величина которого меняется в пределах от 0,7 до 1,2; средняя величина этого коэффициента равна 0,891.
Подъемная сила прямых, полосовых, магнитов, приготовляемых в Гаарлеме, в четыре раза меньше подъемной силы подковообразных магнитов, имеющих тот же вес, что и прямые.
2) Диамагнитные и парамагнитные тела. Давно известно, что, кроме железа, стали, чугуна, магнитными свойствами в сильной степени обладают еще никель и кобальт. Эти металлы в магнитном отношении вполне аналогичны трем первым. В них наблюдается и остаточный М., так что из этих металлов могут быть приготовляемы "постоянные" магниты или, лучше, магнитные стрелки. Давно также было известно, что сильные магниты притягивают к себе многие минералы, содержащие в своем составе соли железа, никеля или кобальта. Но в семидесятых годах прошлого столетия Бругманс заметил совсем противоположное действие магнита на висмут. Из наблюдений Бругманса оказалось, что магнит отталкивает висмут. Впоследствии было обнаружено Беккерелем такое же действие магнита и на сурьму. Как уже изложено в ст. Диамагнетизм, в 1845 г. классическими своими опытами М. Фарадей доказал, что все тела природы — как неорганические, так и органические, как твердые, так и жидкие и газообразные — подчиняются действию магнита, но при этом одни тела притягиваются магнитом или же, будучи подвешены в горизонтальном положении между коническими наконечниками подковообразного электромагнита, устанавливаются своей длиной по направлению оси электромагнита, другие тела, напротив, отталкиваются от магнита или же, будучи подвешены между такими же наконечниками электромагнита, располагаются по направлению экваториальному, т. е. составляющему с осью электромагнита прямой угол. Фарадей назвал тела первой категории парамагнитными, тела второй категории — диамагнитными. Железо является типичным телом первой категории, висмут — второй. Хотя все тела природы испытывают действие магнита, т. е. сами намагничиваются под влиянием магнита так же, как железо, или кажущимся образом по противоположному направлению, остаточное намагничивание наблюдается лишь в немногих телах. За исключением стали, железа, никеля, кобальта, чугуна и некоторых окислов железа, остаточное намагничивание в весьма слабой степени было замечено Тумлирцом в кристаллах кварца и горного хрусталя да еще Лоджем в некоторых металлах и неметаллических телах. При этом во всех этих случаях даже в диамагнитных телах остаточное намагничение обнаруживалось соответствующим парамагнитным телом, т. е. и диамагнитные тела по прекращении действия на них намагничивающей силы являлись с признаками весьма слабо парамагнитных тел.
3) T eopиu магнетизма. Для объяснения или, лучше, для "описания" магнитных явлений была предложена во второй половине прошлого столетия гипотеза, по которой причина всех этих явлений относилась к нахождению в железе и стали особой невесомой материи (materia magnetica, по Эпинусу), обладающей тем свойством, что между ее частицами происходит взаимное отталкивание, а между частицами этой материи и частицами железа и стали существует взаимное притяжение. Это притяжение особенно сильно между частицами магнитной материи и частицами стали, вследствие чего перемещение магнитной материи по порам стали встречает значительное препятствие. Несколько позже была принята другая гипотеза, вполне аналогичная с гипотезой двух электрических жидкостей, предложенной Сеймером. Было допущено существование двух магнитных жидкостей, северной и южной, причем обе эти жидкости предполагались находящимися в равных количествах в телах, способных намагничиваться. Частицы той и другой жидкости отталкивают друг друга, частицы двух разноименных жидкостей друг друга притягивают. Когда тело не намагничено, то, по этой гипотезе, обе жидкости смешаны одна с другой; когда же тело является со свойствами магнита, то обе эти жидкости отделены друг от друга, причем одна из них сосредоточена главным образом на одном конце тела, другая — на другом. Эта гипотеза двух магнитных жидкостей была существенно изменена Кулоном в восьмидесятых годах прошлого столетия. Кулон опытами доказал, что, на сколько бы частей ни был разделен какой— либо магнит, все части его получаются со свойствами целого магнита, т. е. на двух оконечностях каждой такой части наблюдаются противоположные М. Итак, придя к заключению, что вполне невозможно отделение одного М. от другого в противоположность тому, что весьма легко получается с двумя электричествами, Кулон предложил новую гипотезу. Согласно гипотезе Кулона, разделение двух магнитных жидкостей должно происходить лишь в самих частицах намагничиваемого тела и переход магнитных жидкостей из одной частицы в другую вполне невозможен. Таким образом, каждая частица намагниченного тела является, по гипотезе Кулона, цельным магнитиком, т. е. обнаруживает полярность, иначе, обнаруживает на двух противоположных частях своей поверхности разноименные М.
Путем опытов Кулон установил первый количественный закон явлений М. — закон взаимодействия двух количеств М., сосредоточенных в двух телах или в двух элементах объема или поверхности тел. Этот закон, получивший название закона Кулона, лежит в основе математической теории М. Закон Кулона формулируется следующим образом: "действие (f) двух количеств М. (m и m'), воображаемых в двух элементах объема или поверхности намагниченных тел, пропорционально произведению этих количеств и обратно пропорционально квадрату расстояния между ними (r). Это действие направлено по линии соединения рассматриваемых количеств М. и представляет собою взаимное отталкивание, когда оба М. одного рода, и взаимное притяжение, когда они двух различных родов". Итак, закон Кулона выражается формулой:
f = C(mm'/r2)... (1)
Здесь С представляет собой коэффициент, величина которого определяется единицами, принятыми для измерения силы, расстояния и количества М. Принимая за единицу длины сантиметр, за единицу силы дин и полагая в формуле (1) коэффициент С равным единице, мы получаем количества т и т' выраженными в так назыв. абсолютных электромагнитных единицах. Не трудно видеть, что абсолютная электромагнитная единица количества М. представляет собой такое количество М., которое, будучи сконцентрировано в одной точке (в полюсе), отталкивает с силой одного дина равное себе количество одноименного М., также сконцентрированного в одной точке и отстоящего от первого на расстояние одного сантиметра. Нужно прибавить к этому, что оба количества М. должны находиться в одной и той же окружающей их среде, а именно — в воздухе, ибо действие между данными количествами М. меняется с изменением той среды, в которой наблюдается это действие. Правильность закона Кулона была особенно строго доказана опытами Гаусса над действием одного магнита на другой (Gaus s, "Intensitas vis magneticae terrestris ad mensuram absolutam revocata", 1832).
Применяя для вычисления магнитных действий закон Кулона, можно показать, что при всяком данном распределении М., т. е. при всякой данной системе магнитов, сила, какую испытывает от этого распределения М. единица количества М., находящаяся в какой-либо точке, может быть вполне определена как по величине, так и по направлению, если только будет найдено выражение так называемого магнитного потенциала в этой точке. Магнитный потенциал (V) в какой-нибудь точке P представляется в общем виде через
V = ∫(dm/r) ... (2)
Здесь dm означает бесконечно малое количество M., r обозначает расстояние этого элементарного количества М. от точки Р, а интегрирование распространяется на все данное количество М. Обозначая через x, у, z координаты точки P, через X, Y, Z — проекции на оси координат магнитной силы, испытываемой единицей количества М. в этой точке, мы будем иметь
V = f(x, y, z)
X = -dV/dx, Y = -dV/dy, Z = -dV/dz ... (3)
Магнитный потенциал V может быть также рассматриваем, как интеграл дифференциального уравнения
(d2V/dx2) + (d2V/dy2) + (d2V/dz2) — 4 πρ... (4)
в котором обозначает объемную плотность М. в точке x, у, z, т. е. ρ = dm/(dxdydz).
Дифференциальное уравнение (4) выражает собой теорему Пуассона. Для всех точек x, y, z, в которых нет М., т. е. для которых ρ = 0, мы получаем вместо уравнения (4) уравнение
(d2V/dx2) + (d2V/dy2) + (d2V/dz2) = 0... (5).
Это так называемая теорема Лапласа. Магнитный потенциал V, представляющий собою интеграл уравнения (4) или (5), должен в то же время удовлетворять следующему пограничному условию:
(dV/dn1) + (dV/dn2) = -4 πσ ... (6)
Здесь σ обозначает поверхностную плотность М. в какой-нибудь точке поверхности намагниченного тела (т. е. σ = dm/dS, если dS обозначает элемент поверхности), п 1 обозначает нормаль к поверхности в этой точке, проведенную из тела наружу, n2 обозначает нормаль к поверхности в той же точке, проведенную внутрь тела.
Гипотеза Кулона и найденный им закон взаимодействия количеств М. дали возможность Пуассону создать математическую теорию намагничения тел. В своей теории Пуассон, как и Кулон, рассматривает намагниченное тело состоящим из отдельных "магнитных элементов", внутри которых содержатся равные количества двух магнитных жидкостей, отделяющихся одна от другой при намагничивании тела и снова смешивающихся друг с другом, когда тело перестает обнаруживать магнитное состояние. Эти элементы отделены друг от друга промежутками, абсолютно непроницаемыми для магнитных жидкостей. Размеры промежутков и размеры самих магнитн. элементов — одного порядка малости, отношение же между этими размерами различны в различных телах. Отношение суммы объемов всех магнитных элементов тела к объему самого тела Пуассон принимает за меру плотности этого тела относительно М. Чем больше это отношение, этот так называемый Пуассонов коэффициент намагничения k, тем сильнее, согласно рассматриваемой теории, может намагничиваться тело. Для объяснения "постоянного или остаточного М." допускается по этой теории существование в каждом магнитном элементе тела особой "задерживательной силы", противодействующей перемещению магнитных жидкостей в этом элементе. Величина задерживательной силы различна в различных телах. Чем больше эта сила, тем слабее намагничивается тело при действии на него той причины, от которой происходит намагничивание, но зато тем больше получается остаточное намагничение в этом теле.
Если обозначить количество М., являющееся на одном конце магнитного элемента, через m, расстояние между противоположно намагниченными концами этого элемента через ε, число магнитных элементов, находящихся внутри элемента объема тела, через N, то Nm ε будет представлять собой так наз. магнитный момент элемента объема тела. Этот магнитный момент элемента объема может быть выражен иначе, можно положить:
Nm ε = J(dxdydz) ... (7);
здесь dxdydz представляет собою величину элемента объема тела, a J носит название напряженности намагничения в точке, соответствующей центру рассматриваемого элемента объема. Напряженность намагничения J может быть определена так же, как магнитный момент, отнесенный к единице объема тела. Напряженность намагничения вообще изменяется вместе с изменением положения элемента объема в теле, т. е. она выражается некоторой функцией координат х, у, z. Она, кроме того, характеризуется направлением линии, параллельной магнитным осям всех магнитных элементов, заключающихся в рассматриваемом элементе объема. Итак, величина J представляет собой функцию-вектор. Проекции величины J на координатные оси, обозначаемые через А, В , С , называются проекциями напряженности намагничения в точке х, у, z, взятыми на оси координат. Теория Пуассона приводит к следующим выражениям проекций напряженности намагничения А, В, С в зависимости от проекций той силы, какую испытывает единица М., воображаемая в данной точке х, у, z, лежащей внутри исследуемого тела:
| А = [-3k/4 π (1 — k)]d ψ /dx |
...(8) |
| B = [-3k/4 π (1 — k)]d ψ /dy | |
| C = [-3k/4 π (1 — k)]d ψ /dz |
Здесь ψ обозначает полный магнитный потенциал в точке x, у, z, т. е. ψ представляет собою сумму двух потенциалов: потенциала V — от всех внешних магнитов, и потенциала U — от всех магнитных элементов исследуемого тела. Итак, ψ = V + U... (9).
Вводя понятие "напряженность намагничения", мы получаем для потенциала, происходящего от какого-либо магнита, выражение:
V = ∫∫∫[Ad(1/r)/dx + Bd(1/r)/dy + Cd(1/r)/dz]dxdydz ... (10).
Здесь A, B, С обозначают проекции напряженности намагничения в точке х, у, z, лежащей внутри данного магнита; r обозначает расстояние точки х, у, z от той точки, для которой определяется потенциал; интегрирование распространяется по всему объему данного магнита. Выражения (8) показывают, что по теории Пуассона напряженность намагничения в какой-либо точке тела должна возрастать пропорционально увеличению магнитной силы, действующей на единицу М. в этой точке, ибо по этой теории коэффициент k должен представлять собой постоянную величину. Опыты не подтверждают такого вывода. Опыты показывают, что напряженность намагничения всех сильно магнитных тел, каковыми являются железо, сталь, чугун, никель и кобальт, не пропорциональна магнитной силе, но при увеличении последней изменяется весьма сложным образом. Напряженность намагничения каждого такого тела может достигать только некоторой определенной величины, больше которой она не получается, как бы ни была увеличиваема намагничивающая сила. В этом случае говорят, что тело достигло насыщения магнетизмом. Кроме того, при действии одних и тех же магнитных сил напряженность намагничения тела получается весьма различная, смотря по тому, каким намагничениям подвергалось тело раньше (см. Гистерезис).
Итак, теория Пуассона не дает объяснения ни явлению насыщения магнетизмом, ни явлениям магнитного гистерезиса. Она не дает также указаний и на возможность каких-либо механических изменений, происходящих в теле при его намагничении (магнитострикция). Опыты же показывают, что такие изменения происходят и что в некоторых случаях они весьма заметны. Так, опыты обнаруживают изменение длины стержней, приготовленных из сильно магнитных веществ, при намагничении этих стержней. Железные и стальные стержни удлиняются при намагничении, если только магнитная сила, производящая намагничение, не превосходит известного предела. В последнем случае наблюдается укорачивание этих стержней. Никелевые стержни вообще укорачиваются от намагничивания. Стержни из кобальта укорачиваются при небольших намагничивающих силах и удлиняются при больших силах. При намагничении изменяется и объем тела. При намагничении обнаруживаются изменения упругих свойств тела. Так, например, закрученные проволоки несколько раскручиваются при намагничении. Намагничение влияет на электропроводность тел. Особенно сильно это влияние в металле висмуте. Намагничение изменяет также и теплопроводность тела. Оно вызывает и тепловые явления. При прерывистом намагничении какого-либо сильно магнитного тела выделяется весьма заметное количество теплоты (см. Гистерезис). Все эти факты, получаемые из опытов, соответствуют гораздо лучше иной теории М., а именно теории, предложенной Вебером и известной под назв. теории вращающихся молекулярных магнитов. По этой теории, после Вебера измененной несколько Максвеллем и затем дополненной Юингом, каждая частица тела рассматривается как готовый постоянный магнитик. Пока тело не намагничено, все частицы этого тела расположены своими магнитными осями во всевозможных направлениях, вследствие чего, т. е. вследствие такого хаотического распределения осей магнитиков, само тело не может обнаруживать магнитных свойств. Под влиянием намагничивающей силы происходит поворот частичек внутри тела, при чем все частички — элементарные магнитики — стремятся расположиться так, чтобы их одноименные концы были обращены в одну сторону. Чем больше приближаются к параллельности магнитные оси частичек, тем сильнее становится и само тело. Насыщение тела М. получается тогда, когда все частицы расположатся параллельно друг другу и параллельно направлению действующей на тело магнитной силы. Предположение о существовании задерживательной силы, принимаемое в теории Пуассона, может быть заменено, согласно теории вращающихся молекулярных магнитов, допущением существования особого сопротивления в виде, напр., трения, которое встречают частицы при своем повороте. В гипотезе, развиваемой Юингом и дающей возможность до некоторой степени объяснить явления гистерезиса, не предполагается даже и какого-либо трения при изменении положения элементарных магнитиков. Остаточный М., явления гистерезиса, а также и выделение тепла при прерывчатом или переменном намагничивании, объясняются Юингом исключительно на основании принятия во внимание взаимных действий между элементарными магнитиками и возможности, как результат подобных взаимодействий, существования нескольких группировок элементарных магнитиков в теле, группировок, удовлетворяющих условиям равновесия. Для "описательной" математической теории намагничения изотропных тел вполне достаточно допущение, выражаемое формулами:
| A = - κ (d ψ /dx) |
...(11) |
| B = - κ (d ψ /dy) | |
| C = - κ (d ψ /dz) |
в которых А, В, С обозначают проекции напряженности намагничения в точке х, у, z данного тела; ψ обозначает полный магнитный потенциал в этой точке, а κ обозначает магнитную восприимчивость тела в рассматриваемой точке (по Томсону), или коэффициент намагничения (по Нейману). Магнитная восприимчивость κ не представляет собой постоянную величину. Она может меняться при изменении действующей в данной точке тела магнитной силы H (проекции этой силы суть -(dψ/dx), -(dψ/dy), -(dψ/dz), при изменении температуры тела, при изменении давления, претерпеваемого телом, а также она может зависеть и от предшествовавшего магнитного состояния тела. Вместо выражений (11) мы можем написать
J = κН ... (12).
Нужно заметить, однако, что формулы (11) и (12) относятся только к изотропным телам. Теория намагничения кристаллических тел много сложнее. Для кристаллических тел принимаются три главных магнитных восприимчивости х1, х2, х3, соответствующих трем так называемым главным осям намагничения. Весьма важный вывод, получаемый из принятого основного допущения, выражаемого формулами (11), и теоремы Пуассона, заключается в том, что при всяком способе намагничивания изотропного однородного тела свободный М. может явиться лишь на поверхности тела, внутри же этого тела не обнаруживается М., т. е. внутри тела в любой точке сев. и южн. М. взаимно компенсируют друг друга. Итак, для всех точек внутри тела объемная плотность М. (ρ) равна 0. Это может быть выражено иначе, а именно может быть выражено через
(dA/dx) + (dB/dy) + (dC/dz) = 0... (13)
Поверхностная плотность М. (σ) выражается через
σ = κ(dψ/dn) ... (14)
если через n будет обозначена нормаль к поверхности тела, направленная внутрь тела. Магнитный потенциал тела принимает вид
U = ∫∫[κ(dψ/dn)(1/rds)] ... (15).
Здесь dS обозначает элемент поверхности тела, а интегрирование распространяется по всей поверхности, ограничивающей данное тело. Намагничение, при котором внутри тела повсюду ρ = 0, носит название соленоидального намагничения. При таком намагничении является возможность при количественных определениях действий, производимых намагниченным телом, рассматривать это тело как только покрытое поверхностным слоем М., причем этот М. на одной части поверхности тела — сев., на другой — в том же количестве, но южн. Отсюда дальше является возможность ввести понятие о двух магнитных полюсах, т е. таких точках, в которых как бы сосредоточены М., в одном полюсе — сев., в другом полюсе — южн., распределенные в действительности по всей поверхности тела. Эти точки, т. е. магнитные полюсы, представляют собой или точки приложения равнодействующих тех сил, которые действуют на ту или другую часть намагниченного тела, или же эти точки являются как бы центрами, из которых исходят магнитные действия самого тела. Произведение из количества М. в том или другом полюсе на расстояние между полюсами называется магнитным моментом тела. Теория дает следующие выражения для проекций магнитного момента на оси координат:
| Mx = ∫∫∫Adxdydz |
...(16) |
| My = ∫∫∫Bdxdydz | |
| Mz = ∫∫∫Cdxdydz |
Более строгое определение магнитного момента тела будет такое: "магнитный момент тела представляет собою величину момента вращения, испытываемого этим телом, когда оно помещено в пространстве, в котором действующие (на единицу М.) магнитные силы параллельны между собою и по величине равны 1 и при этом магнитная ось этого тела, т. е. линия, соединяющая его полюсы, составляет с направлением магнитных сил прямой угол". Пространство, в котором могут быть обнаружены магнитные силы, носит название магнитного поля. Величина силы, испытываемой единицей М. в какой-либо точке магнитного поля, называется напряжением поля в этой точке (Н). Магнитное поле, во всех точках которого напряжение одинаково как по величине, так и по направлению, называется однородным.
4) Магнитное поле и определение напряжения его. Поверхность, проведенная через те точки магнитного поля, в которых магнитные потенциалы имеют одну и ту же величину, носит название поверхности одинакового магнитного потенциала, или поверхности уровня. Линии, пересекающие все построенные в данном поле поверхности уровня под прямым углом, представляют собою магнитные силовые линии. Касательная, построенная в какой-либо точке такой силовой линии, совпадает с направлением силы, которую испытывает в этой точке северный М., т. е. северный полюс магнита. Напряжение магнитного поля в каком-либо месте его может быть определено числом магнитных силовых линий, пронизывающих единицу поверхности, построенной в этом месте поля под прямым углом к направлению силовых линий. В самом деле, среднее напряжение поля для всех точек, лежащих на поверхности S, может быть выражено через
где ∫∫HdS представляет собою число силовых линий, пронизывающих поверхность S, во всех своих точках перпендикулярную к направлению Н. Магнит, подвешенный горизонтально за свою середину в однородном магнитном поле и выведенный из положения равновесия, приходит в колебание, причем при очень малых амплитудах колебания продолжительность одного полного колебания магнита выражается формулой
Здесь К обозначает момент инерции магнита около оси, совпадающей с нитью подвеса, М обозначает магнитный момент магнита, Н обозначает напряжение поля. Этот же магнит, помещенный под прямым углом к другому магниту, висящему горизонтально в том же однородном поле и притом так, что ось первого магнита своим продолжением рассекает пополам второй магнит (I главное Гауссово положение), а расстояние между серединами магнитов в несколько раз больше длины их, отклоняет второй магнит из его положения равновесия на угол φ, определяющийся формулой
tgφ = 2M/H(1/R3)(1 + U/R2) ... (19).
В этой формуле R обозначает расстояние между серединами обоих магнитов, U обозначает некоторую постоянную величину, зависящую от размеров и намагничения магнитов. Производя отклонение второго магнита первым на двух расстояниях R1 и R2 и измерив в этих двух случаях углы φ1 и φ2, мы из формулы (19) получаем
M/H = ½[(R15tgφ1 - R25tgφ2)/(R12 — R22)]... (20).
Из формулы (18) имеем: МH = 4π2(K/T2) ... (21).
Формулы (20) и (21) дают возможность вычислить как М, так и Н. Таким способом обыкновенно определяется горизонтальная составляющая силы земного М. Определение напряжения магнитного поля между концами электромагнита или в междуполюсном пространстве динамо-магнита производится при помощи других способов. Для этой цели служит или маленькая катушка из проволоки, соединенная с баллистическим гальванометром, или висмутовая плоская спираль. Поместив катушку в магнитное поле так, что плоскости оборотов этой катушки перпендикулярны к направлению силовых линий поля, и затем выдернув эту катушку из поля, наблюдают угол отклонения магнита в гальванометре. Пусть этот угол есть Θ. Наблюдают угол отклонения магнита гальванометра, когда помещенная в общую с катушкой и гальванометром цепь земная рамка, т. е. рамка, около которой обмотано несколько оборотов проволоки, повертывается на 180° около вертикальной оси, проходящей через середину рамки и лежащей в плоскости среднего оборота ее из своего положения, перпендикулярного к магнитному меридиану. Пусть этот угол есть θ. Искомое напряжение магнитного поля вычисляется по формуле Н=2H(Σ/S)[Sin(Θ/2)/sin(θ/2)]. В этой формуле Н обозначает горизонтальную составляющую силы земного M., Σ обозначает сумму площадей всех оборотов земной рамки, S обозначает сумму площадей катушки. При помощи висмутовой спирали напряжение магнитного поля определяется из наблюдения увеличения сопротивления этой спирали, когда она вводится в магнитное поле.
5) Магнитный поток. Вообразив внутри намагниченного тела пещерку, имеющую форму бесконечно тонкого полого диска, перпендикулярного к направлению намагничения тела в этом месте, т. е. перпендикулярного к направлению элементарных магнитиков здесь, и вычислив величину магнитной силы В, какую испытывает единица северного М., воображаемого в центре пещерки, мы получим для случая изотропного тела следующее выражение для B: B=H+4πJ.Так как J=κН, то мы имеем В=(1+4πκ)Н, причем В совпадает по направлению с Н. Величина (1+4πκ), обозначаемая обыкновенно через μ, носит название магнитной проницаемости тела. Величина В называется магнитной индукцией в данной точке (см. Индукция).
Подобно магнитной силе Н, и магнитная индукция В может быть выражена числом линий магнитной индукции, отнесенным к единице поверхности, перпендикулярной к этим линиям. Линии магнитной индукции, касательные к которым совпадают с направлениями магнитной индукции в точках касания, суть линии замкнутые. Пучок таких линий может быть назван магнитным потоком. Число линий, составляющих такой пучок, т. е. величина ∫∫Bdω, если через dω будет обозначен элемент поперечного сечения пучка, может быть названа силой магнитного потока. Нетрудно доказать, что при небольшом сечении (ω) магнитного потока эта сила Z выражается формулой
Z = [∫Hdl]/[∫(1/μ∙dl/ω)]... (22).
Здесь dl обозначает элемент длины магнитного потока, H — магнитная сила, соответствующая точкам элемента dl, а интегрирование распространяется по всему замкнутому потоку. Формула (22) называется "формулой Каппа и братьев Гопкинсонов". Она имеет очень большое применение в электротехнике.
Магнитная проницаемость μ имеет по отношению к магнитным явлениям такое же значение, какое имеет по отношению к явлению электрического тока удельная электропроводность. Магнитная проницаемость парамагнитных тел всегда больше 1, ибо в таких телах магнитная восприимчивость κ > 0. В телах диамагнитных кажущаяся магнитная восприимчивость < 0, а потому для этих тел и кажущаяся μ < 1. Магнитная проницаемость всех тел, за исключением железа, стали, чугуна, никеля и кобальта, весьма близка к 1, так как во всех телах, за исключением сейчас упомянутых, магнитная восприимчивость выражается очень малой дробью. Напр. для наиболее сильномагнитной жидкости, для концентрированного раствора хлорного железа, κ около 0,00005; для воды κ = -0,00000056; для висмута κ = -0,000013; для кислорода κ = 0,0000012. В сильномагнитных телах, каковы железо, сталь, чугун никель и кобальт, магнитная проницаемость выражается сотнями и даже тысячами. В этих телах величина μ не представляется постоянной. Она зависит в весьма значительной степени от величины магнитной силы, действующей на тело. При возрастании этой силы магнитная проницаемость сильно магнитных тел сначала увеличивается, достигает некоторого максимума и потом начинает уменьшаться, асимптотически приближаясь к единице. В следующей таблице приведены величины магнитных сил Н и соответствующих им магнитных проницаемостей железа. Нужно заметить только, что приведенные числа μ для различных Н не относятся к одному и тому же сорту.
| один сорт железа |
Н |
μ |
другой сорт железа |
Н |
μ |
|
1,31 |
245 |
100 |
178,20 |
||
|
1,89 |
370 |
500 |
42,72 |
||
|
2,78 |
920 |
1000 |
22,36 |
||
|
3,36 |
1320 |
||||
|
4,01 |
1600 |
третий сорт железа |
3080 |
7,83 |
|
|
4,95 |
1740 |
10450 |
3,09 |
||
|
5,86 |
1700 |
16390 |
2,25 |
||
|
7,20 |
1570 |
18760 |
2,13 |
||
|
9,14 |
1360 |
24500 |
1,15 |
Во всех телах изменение температуры влияет на величину μ. При некоторой определенной для каждого сильномагнитного тела температуре, так называемой критической температуре, это тело теряет способность намагничиваться. Такая критическая температура для железа различных сортов заключается в пределах от 690° до 870°. Для никеля она близко равна 310°, для кобальта — около 1000°. Всякое механическое действие, которому подвергается тело, также влияет на его способность намагничиваться, т. е. на величину магнитной проницаемости тела. Не обращая внимания на то, что среда, окружающая исследуемое тело, сама способна намагничиваться, мы будем иметь дело с кажущимся намагничением этого тела, а следовательно, будем определять лишь кажущиеся магнитные проницаемость и восприимчивость тела. Теория показывает, что обозначая кажущуюся магнитную восприимчивость исследуемого тела через κ, мы получаем
κ = (κ1 — κ2)/(1 + 4πκ2)... (23).
Здесь κ1 и κ2 суть истинные магнитные восприимчивости данного тела и среды, окружающей это тело. Из формулы (23) видно, что тело будет казаться парамагнитным, когда κ1 > κ2 и, наоборот, тело будет являться со свойствами диамагнитного тела, когда его магнитная восприимчивость κ1 меньше магнитной восприимчивости окружающей среды κ2 (см. Диамагнетизм).
6) Некоторые формулы, относящиеся к намагничиванию тела. Теория дает для энергии намагничения тела, т. е. для той работы, какая должна быть совершена при намагничении этого тела, следующее выражение
W = 1/8π∫∫∫(BHdxdydz)... (24)
или, что то же
W = 1/8π∫∫∫(μH2dxdydz) ... (25).
В этих формулах величины В, Н и μ относятся к одной и той же точке х, у, z, а интегрирование распространяется на объем всего пространства. Из выражения для W можно вывести следующее заключение. При намагничении тела возникают внутри его особые упругие силы. Эти силы по направлению линий магнитной индукции суть силы натяжения, — по направлениям, перпендикулярным к линиям магнитной индукции, суть силы давления. В первом приближении те и другие силы, отнесенные к единице поверхности, могут быть выражены
через F = μ/8πH2... (26).
Тело, намагниченное так, что во всех точках его напряженность намагничения J одна и та же, как по величине, так и по направлению, называется однородно намагниченным. Для такого однородно намагниченного тела магнитный момент выражается через M = Jv. Здесь v обозначает объем тела. Шар, приготовленный из однородного и изотропного вещества, а также и эллипсоид из такого же вещества, помещенные в однородное магнитное поле, причем эллипсоид должен быть расположен так, что одна из его осей совпадает с силовыми линиями поля, намагничиваются однородно. Точно так же намагничивается однородно в однородном магнитном поле и очень длинный стержень, если этот стержень сам однородный и изотропный и если он находится в магнитном поле в положении, при котором ось стержня совпадает с силовыми линиями поля. Теория дает следующие выражения для напряженности намагничения в случае однородного намагничения.
Для шара J = (κ/[1 + 4/3πκ])H ... (27).
Для удлиненного эллипсоида вращения, причем ось вращения параллельна силовым линиям поля J = [κ/(1 + κN)]H... (28).
В последней формулe N представляет собой следующее:
N = 4π(1/e2 — 1)[(1/2elg(1 + e)/(1 — e)) — 1]
и е обозначает эксцентриситет эллипсоида. В обеих формулах (27) и (28) величина Н есть напряжение магнитного поля, в которое введены исследуемые тела. Так, в том случае, когда магнитное поле возбуждается внутри длинной катушки, по проволоке которой проходит ток силою i, величина Н вычисляется по формуле: Н = 4πn1i, причем в этой формуле п1 обозначает собой число оборотов катушки, приходящееся на единицу длины ее.
Магнитная сила Н, действующая внутри тела, выражается следующим образом:
для шара Н = [1/(1 + 4/3πκ)]Н,
для удлиненного эллипсоида Н = [1/(1 + κN)]H.
Итак, размагничивающая сила, появляющаяся внутри однородного
намагниченного шара, выражается через
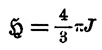 ;
размагничивающая сила, появляющаяся внутри однородно намагниченного
удлиненного эллипсоида, выражается через
;
размагничивающая сила, появляющаяся внутри однородно намагниченного
удлиненного эллипсоида, выражается через
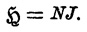 . Магнитный
момент однородно намагниченного эллипсоида вычисляется по формуле: M =
4/3πabcJ. Здесь а, b, с суть полуоси
эллипсоида. Если эллипсоид однородно намагничен по направлению, параллельному
его оси 2а, то полюсы в таком эллипсоиде расположены на этой же оси в
расстоянии 1/3а от концов ее. В магнитах, имеющих
форму прямых стержней или полос, распределение свободного М. по
поверхности магнита может быть выражено следующей данной Био формулой:
. Магнитный
момент однородно намагниченного эллипсоида вычисляется по формуле: M =
4/3πabcJ. Здесь а, b, с суть полуоси
эллипсоида. Если эллипсоид однородно намагничен по направлению, параллельному
его оси 2а, то полюсы в таком эллипсоиде расположены на этой же оси в
расстоянии 1/3а от концов ее. В магнитах, имеющих
форму прямых стержней или полос, распределение свободного М. по
поверхности магнита может быть выражено следующей данной Био формулой:
σ = a(bx — b2l-x)... (29).
В этой формуле σ обозначает плотность М. в точке, отстоящей на расстоянии x от одного конца магнита; а и b суть некоторые постоянные величины, a 2l длина магнита. Как видно из формулы (29), на середине магнита σ = 0. На середине магнита получается пояс безразличия. Более подробное изложение теории М. см. в сочинении "Основания учения об электрических и магнитных явлениях" И. И. Боргмана.
И. Боргман.