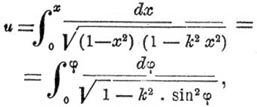
Модуль математический
— слово, употребляемое математиками в значениях весьма разнообразных. В теории упругости: опыт показал, что удлинение l, производимое силою P в призматическом или цилиндрическом теле, пропорционально силе P и первоначальной длине L и обратно пропорционально площади s поперечного сечения, так что эти величины связаны формулою l = (PL)/(ES), где E есть некоторый коэффициент, имеющий для различных тел различные величины и характеризующий растяжимость данного тела. Этот коэффициент и называется модулем упругости. Если положить s = 1 и l = L, то приведенная формула дает E = Р. Итак, модуль упругости данного материала есть та сила, под действием которой призматическое тело, сделанное из этого материала, имеющее площадь поперечного сечения, равную единице, удлинилось бы вдвое, если бы предварительно не изменило своей растяжимости или не лопнуло бы (см. Упругость). В теории мнимых величин: модулем величины х + у √(—1)
называется величина √(х 2 + у 2); если же мнимая величина (см.) выражена в виде
r (cos φ + sin φ √(—1)),
то r есть ее модуль. В теории чисел: если разность чисел a и b делится на число т без остатка, то говорят, что а сравнимо с b по модулю m, выражая это в виде так называемого сравнения: а = b (Mm). Итак, модулем сравнения между числами а и b называется точный делитель разности a — b. В теории эллиптических функций модулем называется величина k в эллиптическом интеграле
в котором φ называется амплитудою и, причем основными эллиптическими функциями от и называются:
sin φ = snu = синус амплитуды
cos φ = csu = косинус амплитуды
Δφ = dnu = дельта амплитуды.
Эти функции; вытекая из обращения эллиптического интеграла, зависят от аргумента и и от модуля k. Величина √(1 — k2) называется дополнительным модулем. В теории логарифмов модулем называется число, на которое нужно умножить логарифм данной системы, чтобы получить логарифм другой системы (см. Логарифм).
Н. Делоне.