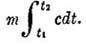
Термохимия
— отдел химии, занимающийся превращениями внутренней энергии тел в тепло при химических процессах. Почти каждая химическая реакция связана с тем или иным тепловым эффектом: химическое превращение сопровождается или выделением, или поглощением тепла. В первом случае реакция называется экзотермической, во втором — эндотермической. Тепловой эффект реакций является мерилом изменения внутренней энергии тел, участвующих в химическом превращении. Взаимные превращения различных видов энергии составляют предмет термодинамики, установившей законы таких превращений; поэтому в основе Т., занимающейся одним из видов таких превращений, лежат законы термодинамики, приложение которых к химическим явлениям и составляет содержание Т. Соответственно этому, дальнейшее изложение разделено на три части: очерк развития Т., приложения I закона и приложения II закона термодинамики.
История термохимии. До Лавуазье тепловой эффект химических реакций объяснялся выделением или поглощением флогистона (см. Флогистон). Лавуазье, показавшему отличие между материей весомой и невесомой, т. е. между тем, что называется теперь веществом, и различными видами энергии, принадлежат и первые термохимические исследования (теплоты горения и теплоты, выделяемой животными), произведенные им совместно с Лапласом с помощью ледяного калориметра. Из теоретических воззрений Лавуазье и Лапласа имеет значение положение, принимавшееся ими за аксиому, что при разложении химического соединения на его составные части затрачивается столько же тепла, сколько его выделяется при образовании этого соединения. Другие исследователи в области Т., работавшие в конце XVIII и начале XIX стол., как то: Крауфорд, Румфорд, Дэви, Дальтон, Дюлонг, Депре, не дали научных оснований для Т. Истинным основателем Т. явился Гесс в своих работах, напечатанных в изданиях Петербургской акад. наук в 1839—1844 гг. Закон постоянства сумм тепла, установленный им в 1840 г. и гласящий, что выделение тепла, сопровождающее химическую реакцию, всегда одно и то же независимо от того, протекает ли реакция сразу, или она разбивается на ряд промежуточных реакций, является основным законом Т. Не останавливаясь на других выводах и обобщениях Гесса, опровергнутых позднейшими исследователями, замечу, что он указал на явление термонейтральности (см. дальше), хотя и дал ему неверное объяснение. Андрюс и Грэм в современных Гессу работах дали кое-какой фактический материал, не давши ничего теоретическому развитию Т.; еще меньшее значение имели работы Ходнева, Абриа, Грасси, Вуда, числовые данные которых крайне неточны, а подчас и прямо неверны. Новый толчок в развитии Т. дали Фавр и Зильберман, 1852—53. Новые методы калориметрических определений (см. Калориметрия) и множество разнообразных химических реакций, тепловые эффекты которых были изучены названными исследователями, обеспечили за ними выдающееся место в среде термохимиков. Менее удачны были их теоретические объяснения наблюденных фактов. Правда, они дали правильное объяснение явлению термонейтральности, зато в других случаях они не могли отрешиться от господствовавших тогда неверных взглядов. Так, общепринято было мнение, что всякая реакция соединения сопровождается выделением тепла, и обратно, — при разложении тепло поглощается. Фавр и Зильберман, первые нашедшие соединения, разлагающиеся с выделением тепла, именно сернистый углерод, закись азота и перекись водорода, старались объяснить такое явление аллотропическим изменением элементов перед образованием соединения и при разложении его, считая, что сама реакция соединения все же идет с выделением тепла. Фавру же и Зильберману принадлежит открытие различных теплот горения для различных аллотропических состояний углерода и серы. Таково было положение Т. до появления работ Томсена, который был первый термохимик, применивший механическую теорию тепла к химическим явлениям. В своей статье, появившейся в 1853 г. ("Grandz ü ge eines thermochemischen Systems", "Poggendorff's Annalen", т. 88), он, исходя из первого закона термодинамики, закона сохранения энергии, следующим образом формулирует основные принципы Т. При этом надо заметить, что терминология Томсена отличается от употребляемой ныне: он говорить "сила" вместо работа или энергия. Интенсивность химической силы (запас химической энергии) одного и того же тела при неизменной температуре есть величина постоянная. При превращении тела в другое, отличающееся от первого термохимически, т. е. обладающее другим запасом химической энергии, развивается некоторая работа. Эта работа может быть измерена: она есть не что иное, как выделяющееся при реакции тепло. Поэтому все количество тепла, образующееся при химической реакции, есть мера развитой процессом химической силы (работы). Алгебраическую сумму количеств тепла выделенных и поглощенных при реакции, причем выделенное тепло принимают за величину положительную, поглощенное — за отрицательную, Томсен назвал тепловым эффектом (Wärmetö nung) реакции. Представляя себе, что запас химической энергии вещества может быть использован целиком, полученное таким образом количество тепла, измеренное в единицах количества тепла (калориях) и отнесенное к эквивалентному весу вещества, Томсен назвал термохимическим эквивалентом. Величина теплового эффекта образования химического соединения есть разница между суммой термохимических эквивалентов веществ, образующих соединение, и термохимическим эквивалентом образовавшегося соединения. Из этого принципа видно, что тепловой эффект реакции не зависит от того, тем или иным путем идет реакция, лишь бы исходные вещества и продукты реакции были одни и те же; а это и есть сущность закона Гесса. Таким образом, Томсен выводит закон Гесса из первого закона термодинамики. В 1854 г. Томсен высказывает следующий принцип: каждый простой или сложный чисто химический процесс сопровождается выделением тепла. Этот принцип гипотетического характера является первой попыткой предсказания при помощи теплового эффекта направления хода химической реакции. Но уже сам Томсен, применяя этот принцип, натолкнулся на противоречащие ему факты. С 1865 г. стали появляться статьи Бертело, в которых он, независимо, по-видимому, от Томсена, выводит основные законы Т. Окончательная форма, в которую вылилось применение первого закона термодинамики к химическим явлениям, выражена им в следующих двух принципах. I. Принцип молекулярных работ: количество тепла, выделенное какой-нибудь реакцией, есть мера совокупности химических и физических работ, совершенных в этой реакции. II. Принцип термической эквивалентности химических превращений, или иначе — принцип начального и конечного состояний: если система простых или сложных тел, взятая в определенных условиях, претерпевает физические или химические превращения, способные привести ее к новому состоянию, не сопровождаясь при этом никаким внешним по отношению к системе механическим эффектом, количество выделенного или поглощенного этими превращениями тепла зависит только от начального и конечного состояний системы; количество тепла одно и то же, каковы бы ни были природа и порядок промежуточных состояний. В своих исследованиях Бертело подробно разрабатывает влияние на тепловой эффект превращений различных факторов, именно влияние агрегатного состояния веществ, участвующих в реакции, влияние внешней механической работы, производимой системой во время превращения и влияние температуры. Последнее, т. е. влияние температуры на тепловой эффект химических реакций, впервые было указано Кирхгоффом уже в 1858 г. На этом заканчивается теоретическое развитие применения закона сохранения энергии в Т. — Томсену и Бертело принадлежит также и заслуга разработки экспериментальной стороны Т. После отдельных экспериментальных исследований, произведенных в пятидесятых годах, Томсен начинает в 1869 г. обширнейшие, по строго систематическому плану, работы, результаты которых собраны в четырех томах, изданных в 1882—1886 гг. ("Thermochemische Untersuchungen"). В 1875 г. Бертело начинает свои исследования и ведет их без перерыва и по настоящее время; числовой материал работ Бертело и его многочисленных учеников публикуется в "Annales de chimie et de physique" и собирается в "Essai de m écanique chimique fondée sur la therm ochimie", 1879, и в "Thermochimie. Donn ées et lois numé riques", 1897 г. Эти исследователи совершенствуют известные и разрабатывают новые калориметрические методы и методы термохимического исследования всевозможных реакций. Взаимная проверка исследователей дает высокую степень точности огромной массе собранного ими материала. При этом надо заметить, что данные Томсена, полученные все при 18°, имеют преимущество в смысле большой сравнимости перед данными Бертело, производившего свои определения в пределах температур между 10° и 20°.
Изучение теплового эффекта химических превращений поставило на очередь вопрос о том, какая из возможных для взятых тел реакций будет иметь место при данных условиях. Выше уже было указано, что Томсен в 1854г. пытался это сделать, говоря, что каждый простой или сложный чисто химический процесс сопровождается выделением тепла. На основании этого положения только экзотермическая реакция идет непосредственно, сама по себе, реакции же эндотермические могут быть воспроизведены лишь окольным путем. Этим же вопросом занялся и Бертело. Подходя к решению его постепенно в первых своих исследованиях по Т., он в 1873 г. окончательно сформулировал свой третий принцип Т., принцип максимальной работы: всякое химическое превращение, совершающееся без участия посторонней энергии, ведет к образованию тела или системы тел, выделяющих наибольшее количество тепла. Этот принцип Бертело кладет в основу химической механики, посвящая, между прочим, его применению второй том своего "Essai de m écanique chimique". Соображения, посредством которых Бертело вывел свой принцип максимальной работы, основаны на законе сохранения энергии. Это можно заключить из следующих его слов: "необходимость этого принципа видна из того, что система, выделившая наибольшее возможное количество тепла, не обладает сама по себе запасом энергии, необходимой для нового превращения. Всякое новое превращение требует затраты работы, не могущей быть произведенной без участия посторонней энергии. Наоборот, система, способная еще выделить тепло при новом превращении, заключает в себе энергию, необходимую для этого превращения безо всякой посторонней помощи". Согласуясь во многих случаях с фактами, принцип максимальной работы оказался неприменимым к целому ряду данных опыта. Уже Томсену пришлось встретиться с такими противоречиями: так, он нашел, что хлористый водород не реагирует с серебром и ртутью, хотя эти реакции должны выделять значительное количество тепла. В других случаях реакции идут с поглощением тепла. Дальнейшие исследования разных ученых указывали все большее и большее число случаев, когда принцип максимальной работы оказывался неприменимым. Все такие противоречия Бертело старался объяснить участием посторонней энергии: света, электричества в виде гальванического тока, тихого разряда или искры, энергии дезагрегации, развиваемой растворением. Работы Сент-Клэр-Девилля и его учеников над диссоциацией при высоких температурах, показавшие, что в этих условиях разлагаются прочнейшие химические соединения, образующиеся с выделением громадных количеств тепла, как, напр., вода и хлористый водород, заставили Бертело причислить к числу внешних энергий и тепло. Этим Бертело отнял у своего принципа его значение: если всякое химическое превращение, совершающееся без участия посторонней энергии, выделяет тепло, то, принимая во внимание, что участие тепла как посторонней энергии выражается поглощением тепла, — мы получим следующее выражение для частного случая применения принципа максимальной работы: всякое химическое превращение, идущее без поглощения тепла, выделяет тепло. Основная ошибка Бертело была та, что он положил в основание своего принципа максимальной работы первый закон термодинамики, закон сохранения энергии. На самом деле этот закон совершенно не касается вопроса о направлении протекающих в природе процессов; вопрос этот составляет содержание второго закона термодинамики. Так, в случае двух тел различной температуры, с помощью теплопроводности обменивающихся теплом, закон сохранения энергии требует только, чтобы количество тепла, отданное одним телом, было равно количеству тепла, принятому вторым; и только II закон указывает, что отдает тепло тело с высшей температурой, а принимает — тело с более низкой температурой. Направление процесса обусловливается изменениями не энергии, а энтропии системы. В то время, когда Бертело разрабатывал свой неверный принцип, появилась в анналах Либиха за 1873 г. статья Горстмана о теории диссоциации. В этой статье в первый раз II закон термодинамики был приложен к химическим явлениям. Выводы Горстмана следующие: при диссоциации равновесие наступает тогда, когда энтропия приняла наибольшую из возможных при данных превращениях величину. Вообще, говорит он, возможно только такое химическое превращение, при котором энтропия увеличивается. Эти положения не были изменены дальнейшими исследованиями. Разработка их повела к более детальному приложению II закона термодинамики к химическим явлениям, выяснению влияния различных факторов на направление химического превращения и к изучению химических равновесий, чем были положены основы современной химической механики. Классическими в этой области явились исследования Гиббса, "On the equilibrium of heterogenous substances" в "Tran s actions of Connecticut Academy" (т. III, 1875) и Гельмгольца, "Zur Thermodynamik chemischer Vorg änge " в "Sitzungsberichte der Berliner Akademie" (1882). Необходимо также указать имена Мутье, Робэна, Вант-Гоффа, Лешателье и Дюгема, внесших свою долю в разработку отдельных сюда относящихся вопросов.
Приложения I закона термодинамики. В предыдущем были указаны принципы, основанные на законе сохранения энергии и применявшиеся в Т. Здесь мы изложим их так, как они применяются в настоящее время — в крайне простом и сжатом виде. Закон сохранения энергии для случая превращения внутренней энергии в тепло и механическую работу выражается уравнением: dU = dQ + dr, где: dU — изменение внутренней энергии системы, dQ — выделенное или поглощенное системой тепло, a dr — внешняя, механическая работа, произведенная системой. Во всех случаях, когда в реакции не участвуют газы, внешняя работа dr может быть опущена благодаря ничтожной величине ее. Уравнение превращается в dU = dQ и после интегрирования получается: U1 — U2 = Q, где U1 — внутренняя энергия начального, а U2 — внутренняя энергия конечного состояния системы, Q — тепловой эффект превращения. В Т. принято считать величину Q положительной, когда превращение совершается с выделением тепла. В более наглядной форме: U1 = U2 + Q выражает, что внутренняя энергия тел до реакции равна внутренней энергии тел после реакции плюс выделенное системой тепло. Это есть простейшее выражение закона Гесса и первых двух принципов Бертело. Определение величины Q производится калориметрически, что описано подробно в статье Калориметрия (см.). Единицы тепла приняты в Т. следующие: 1) малая калория — количество тепла, требуемое для нагрева 1 грамма воды от 0° до 1°, она обозначается cal.; 2) большая калория, введенная Бертело и равная 1000 малым, обозначается Cal. В Германии по предложению Оствальда употребляются 3) новая калория Шюллера и Варта, равная количеству тепла, нужному для нагрева 1 грамма воды от 0° до 100°; она равна 100 малым калориям, соответствующим количеству тепла, необходимому для нагрева 1 грамма воды на 1° при температуре, близкой к 18°, т. е. температуре громадного большинства термохимических определений. Новая, или, как ее часто называют, средняя калория обозначается К; 4) наконец, в 1899 г. Оствальд в своем "Grundriss der allgemeinen Chemie" вводит калорию, основанную на абсолютной системе С. G. S. единиц, именно "джоуль", обозначаемый j; j = 0,2391 cal. = 10 7 эргов. 1 cal. = 4,183 j. Более удобна для практического применения единица, в 1000 раз большая: J = 239,1 cal. = 10 10 эргов. Все термохимические определения относятся к грамм-молекулярным количествам веществ. Для выражения результатов термохимических определений предложены особые приемы. Наиболее употребительны томсеновский и оствальдовский. Томсен ставит химические формулы реагирующих веществ рядом, разделяя их запятыми и заключая все в скобки; знак равенства соединяет это выражение с тепловым эффектом реакции. Так (Н,Сl) = 22001 cal. — обозначает, что соединение 1 грамма водорода с 35,46 граммами хлора выделяет 22001 cal. Оствальдовское обозначение не столь сокращенно, зато представляет больше систематичности и удобства для расчетов. Он употребляет обыкновенно химическое равенство, прибавляя ко второй части тепловой эффект реакции; при этом химические формулы обозначают не только атомные количества, но и запас внутренней энергии соответствующих тел. Для разных агрегатных состояний употребляется различный шрифт: обыкновенный для жидкого, жирный для твердого и курсив для газообразного. Иногда вместо разных шрифтов употребляют разные скобки: формула жидкого вещества заключается в скобки — (), твердого — [], газообразного — {}. В случае, когда тела берутся при другой температуре, чем обычная в 18°, подле формулы в скобках ставится температура. Так, (Н 2O)(0) = [Н 2O](0) + 14,4 К обозначает, что 18 грамм воды, превращаясь при 0° в лед, выделяют 14,4 К. С оствальдовским выражением можно обращаться, как с алгебраическим уравнением, перенося члены из одной части в другую с переменой знака, складывая или вычитая почленно одни уравнения с другими. При всяких обозначениях в реакциях, идущих в растворах при разбавлениях, когда дальнейшая прибавка растворителя не вызывает заметного теплового эффекта, принято растворитель обозначать особым выражением: aq. для воды, alc. для алкоголя и т. д. Так, образование хлористого калия из едкого кали и хлористого водорода, причем все вещества взяты в растворах, пишется — по Томсену: (KOHaq, HClaq) = 13700 cal.; по Оствальду: KOHaq + HClaq = KClaq + Н 2 O + 137 К.
Влияние температуры на тепловой эффект выражается следующим образом: тепловой эффект реакции Qt2 при какой-нибудь температуре t2 равен тепловому эффекту Qt1, определенному при другой температуре t1, увеличенному на произведение разницы сумм молекулярных теплоемкостей веществ до и после реакции, помноженной на разницу температур. Если обозначить через с' теплоемкость, а через m' молекулярный вес каждого вещества, вступающего в реакцию, через с и m те же величины для отдельных продуктов реакции, вышеуказанное положение примет следующий вид:
Qt2 = Qt1 + (Σ m'c' — Σ mc)(t2 — t1).
В случае, если величины теплоемкостей меняются с температурой, то необходимо или брать средние теплоемкости между температурами t1 и t2, или, выражая теплоемкость функцией температуры, заменить каждый член mc(t2 — t1) соответствующим интегралом
Влияние внешней работы на тепловой эффект. Выше было указано, что, если в реакции не участвуют газообразные вещества, внешняя работа может не приниматься в расчет ввиду ее ничтожной величины. Если же при реакции выделяются или поглощаются газы, то необходимо ввести соответствующую поправку. В обычных условиях, когда реакция ведется при постоянном атмосферном давлении, зависимость между истинным тепловым эффектом реакции Q и наблюденным при постоянном давлении Qp выражается уравнением:
Q = Qp — 2(n' — n)T саl., где T — абсолютная температура реакции; n' и n — число грамм-молекул газа до и после реакции; 2 — константа R уравнения состояния газов pv = RT. Величина внешней работы не зависит от давления, если только во время реакции давление остается постоянным. В тех случаях, когда реакция ведется при постоянном объеме, как это имеет место в калориметрической бомбе Бертело, внешняя работа газа равна нулю и наблюдаемый тепловой эффект равен истинному.
Определения теплового эффекта косвенным путем. Очень часто по тем или иным причинам тепловой эффект реакции не может быть определен непосредственно. В таких случаях его вычисляют из тепловых эффектов, непосредственно определенных для нескольких реакций, подобранных таким образом, чтобы, если бы они были произведены последовательно, то в результате получилось бы то превращение веществ, тепловой эффект которого требуется определить. Для пояснения приведем пример. Теплота образования окиси углерода из элементов не может быть определена непосредственно; известны теплоты горения углерода в углекислоту и окиси углерода в углекислоту. Если сжечь сперва уголь в углекислоту, а затем разложить полученную углекислоту на СО и кислород, то, очевидно, результат этих двух реакций выразится: С + О = СО. Тепловой эффект последней реакции получим, вычтя из теплоты горения углерода в углекислоту теплоту горения окиси углерода в углекислоту, так как последняя имеет ту же величину, но с обратным знаком, как теплота разложения СО 2 на кислород и СО. С помощью Оствальдовского обозначения такие расчеты производятся крайне просто. Написав, что при постоянном объеме:
С + 2O = СО 2 + 97000 cal.
СО + О = СО 2 + 68000 cal.
и вычтя почленно второе уравнение из первого, получим искомый результат: С + О = СО + 29000 cal. Для вычислений тепловых эффектов всевозможных реакций с помощью имеющихся уже термохимических данных пользуются расчетом по теплотам образования сложных веществ из элементов. Расчет производится на основании правила: тепловой эффект реакции равен разности суммы теплот образования продуктов реакции и суммы теплот образования веществ до реакции. Так, подписывая под веществами их теплоты образования, находим для реакции
тепловой эффект равным 239800 cal. Для целей таких расчетов в справочных книгах термохимические данные приводятся в виде теплот образования из элементов, причем для каждого вещества даются числа: для твердого, жидкого, газообразного и растворенного (в воде) состояний.
Теплоты растворения и разбавления. Теплота растворения определенного количества (грамм-молекулы) вещества зависит от количества взятого для растворения растворителя, иначе говоря, от концентрации образующегося раствора. При постепенном увеличении количества растворителя теплота растворения достигает некоторой величины, не изменяющейся при дальнейшем прибавлении растворителя. Эта предельная величина называется теплотой растворения при бесконечном разведении, иногда же, что хуже, просто теплотой растворения. Достигается этот предел для разных веществ при различных количествах растворителя; обыкновенно, чем больше величина теплоты растворения, тем дольше лежит предел. Так, для аммиака NH 3, выделяющего при бесконечном разведении 88 K., предел уже достигнут, когда образовался раствор состава NH 3 ·50Н 2 O, для хлористого водорода НСl, выделяющего 174 K., — предел лежит при образовании раствора HCl·200H 2 O, для серной кислоты H 2SO4 при выделении 892 K. предел еще не достигнут при растворе Н 2 SО 4 ·800Н 2 O. В последнее время в химической механике стала употребляться иногда другая величина, теплота растворения до насыщения, соответствующая теплоте растворения вещества в таком количестве растворителя, чтобы образовался насыщенный раствор. Теплота разбавления раствора от большей концентрации к меньшей есть разность теплот растворения при меньшей и при большой концентрациях. Теплота концентрирования раствора есть величина, обратная теплоте разбавления, наблюдаемая при растворении в данном растворе новых количеств растворенного тела, что ведет к увеличению концентрации раствора.
Теплоты растворения газов. При растворении в жидкостях газы распадаются на две резко отличающиеся группы. Газы, следующие закону Генри, т. е. такие, растворимость которых увеличивается пропорционально давлению, дают при растворении столь незначительный тепловой эффект, что он не мог быть еще до сих пор определен. Газы, не следующие закону Генри, имеют значительные положительные величины теплот растворения, превышающие теплоты сжижения их. В следующей таблице приведены теплоты растворения в воде при бесконечном разведении Q некоторых газов и паров при температуре 15—20° и их теплоте сжижения q.
|
QK. |
qK. |
QK. |
qK. |
QK. |
qK. |
|||
| Cl2 |
30 |
— |
HNO3 |
144 |
73 |
СН 3 —СО 2H |
76 |
73 |
| Br2 |
83 |
72 |
SO2 |
77 |
62 |
СН 3 —СОН |
89 |
60 |
| НСl |
174 |
— |
Сl 2O |
94 |
— |
СН 3 —СН 2 OН |
124 |
98 |
| HBr |
200 |
— |
СО 2 |
58 |
61 |
(C2H5)2O |
126 |
67 |
| HJ |
194 |
— |
COCl2 |
580 |
— |
CH3—CO2(C2H5) |
140 |
109 |
| H2S |
47 |
— |
COS |
68 |
— |
(C2O4)(C2H5)2 |
337 |
106 |
| NH3 |
88 |
44 |
HCN |
61 |
57 |
CHCl3 |
95 |
73 |
| NO2 |
78 |
43 |
HCO2H |
57 |
56 |
ССl 3 —СОН |
199 |
80 |
Поглощение газов твердыми телами также сопровождается положительным тепловым эффектом. В случае пористых, обладающих большой поверхностью твердых тел, при значительном объеме поглощенного газа выделяются значительные количества тепла, в большинстве случаев превосходящие теплоты сжижения. Так, 100 г платиновой черни, поглощая 0,1 г водорода, выделяют 414 К. При поглощении углем более плотные сорта угля, поглощая меньше газа, чем менее плотные сорта, выделяют на одно и то же количество газа большие количества тепла. Первые порции поглощенных газов выделяют больше тепла, чем последние.
|
Газы |
Выделенное тепло |
||
|
при различных условиях |
до насыщения |
Теплота сжижения |
|
| NH3 |
49—88 К. |
84 К. |
44 К. |
| НС1 |
92—102 |
100 |
— |
| HBr |
— |
155 |
— |
| HJ |
— |
220 |
— |
| SO2 |
10—110 |
108 |
56 |
| СО 2 |
66—78 |
70 |
61 |
| N2O |
72—76 |
74 |
44 |
Теплоты растворения жидкостей друг в друге имеют обыкновенно положительные величины. В случае растворения в воде органических веществ тепловой эффект бывает незначителен; сильные неорганические кислоты, наоборот, дают гораздо большие величины.
В следующей таблице приведены некоторые относящиеся сюда данные для теплот растворения при бесконечном разведении.
| QK | |
| CH3—OH |
20 |
| C2H5—OH |
25 |
| C3H7 —OH н. |
31 |
| C3H7 —OH изо. |
35 |
| C4 Н 9 —ОН изо. |
29 |
| С 5H11 —ОН изо. |
28 |
| C3H5(OH)3 |
15 |
| (CH3)2CO |
25 |
| СН 2 =СН—СН 2 —ОН |
21 |
| C2H5—COH |
40 |
| CH3—COH |
36 |
| ССl 3 —СОН |
119 |
| (C2H5)2 Ο |
59 |
| ΝΟ 3(C2 Η 5) |
10 |
| СН 3 —СО 2(C2 Н 5) |
31 |
| (С 2O4)(C2H5)2 |
31 |
| НСО 2H |
1 |
| CH3—CO2H |
4 |
| C3H7—CO2H |
10 |
| С 4H9 —СО 2H |
8 |
| HCN |
4 |
| HNO3 |
72 |
| H2SO4 |
89 |
Для азотной и серной кислот Томсен дал эмпирические формулы для теплот растворения
(Н 2SO4, nН 2O) = [n/(n + 1,798)]178,6 К.; формула годна для n от 0 до 20.
(HNO3, nН 2O) = [n/(n + 1,737)]89,74 К.;
формула годна для n от 0 до 5.
Теплоты разбавления неорганических сильных кислот уменьшаются по мере увеличения содержания воды в разбавляемом растворе. Для азотной кислоты теплота разбавления, будучи сперва положительной, уменьшаясь, меняет знак и становится отрицательной, т. е. разведение слабых растворов HNO 3 идет с поглощением тепла. Для теплот разбавления растворов галоидоводородных кислот имеются эмпирические формулы:
(НСlnН 2O, aq) = 119,8/n К.
(НВrnН 2O, aq) = [(120,6/n) — 2] К. до n = 40;
при n > 40, Q = 120,6/n К.
(HJnН 2O, aq) = [(1174/n) — 5] К. до п = 20;
при n > 20, Q = 19,57/n К.
Крайне своеобразно изменение теплот растворения этилового алкоголя в воде с повышением температуры. Теплоты растворения грамм-молекулы C 2H5 OH в таких количествах воды, чтобы образовался раствор с содержанием р % алкоголя, следующие:
|
р %. |
Q.K. |
p %. |
Q.K |
|
90 |
0,787 |
30 |
14,71 |
|
80 |
1,435 |
20 |
20,22 |
|
60 |
4,18 |
10 |
24,55 |
|
40 |
10,32 |
При повышении температуры теплоты растворения понижаются пропорционально их величинам так, что при температурах кипения спирто-водных растворов теплоты образования этих последних из жидких воды и алкоголя становятся равными нулю.
Теплота растворения твердых тел. Наиболее важным фактором, влияющим здесь на величину теплового эффекта, является способность растворенного вещества образовать соединения с растворителем, в случае растворения в воде — способность образовать кристаллогидраты. Вещества, не образующие кристаллогидратов, стойких при обыкновенной температуре, при которой производится определение теплоты их растворения, растворяясь в воде, почти без исключения поглощают тепло. Как примеры можно привести:
| (KCl, aq) | = —44,4 К. |
| (NaCl, aq) | = —11,8 К. |
| (KNO3, aq) | = —85,2 К. |
| (K2SO4, aq) | = —31 К. |
| [(NH4)2SO4, aq] | = —12 К. |
| (KClO3, aq) | = —100 К. |
| (NaClO3, aq) | = —56 К. |
| (KClO4, aq) | = —121 К. |
| (KMnO4, aq) | = —104 К. |
Сюда же относится целый ряд органических соединений.
Соединения, образующие кристаллогидраты, будучи в безводном состоянии, в большинстве случаев выделяют тепло. Растворение соответствующего безводному веществу кристаллогидрата сопровождается всегда меньшим выделением тепла, очень часто даже — поглощением. Теплота растворения для веществ, способных образовать несколько кристаллогидратов, тем меньше, чем больше содержание воды в растворяемом кристаллогидрате. Ряд нижеследующих примеров наглядно поясняет эти положения:
| (KHO, aq) | = 124,6 К. |
| (KНО·H 2 O, аq) | = 36 К. |
| (NaНО·2H 2 O, аq) | = —0,3 К. |
| (NaHO, aq) | = 97,8 К. |
| (NaHO·H2O, aq) | = 65 К. |
| (Ba(OH)2, aq) | = 102 К. |
| (Ва(OH) 2·9H2 O, аq) | = —142 К. |
| (Sr(ОН) 2, aq) | = 96 К. |
| (Sr(ОН) 2·9H2O, aq) | = 150 К. |
| (NaBr, aq) | = —2 К. |
| (NaBr·2H2O, aq) | = —47 К. |
| (CaCl2, aq) | = 174,1 К. |
| (СаСl 2·6H2O, aq) | = — 43,4 К. |
| (MgSO4, aq) | = 202,8 К. |
| (MgSO4·7H2O, aq) | = —38 К. |
| (Sr(NO3)2, aq) | = —46 К. |
| (Sr(NO3)2·5H2O, aq) | = —122 К. |
| (Na(C2H3O2), aq) | = 42 К. |
| (Na(C2H3O2)·6H2 O, аq) | = —96 К. |
| (Na2SO4, aq) | = 4,6 К. |
| (Na2SO4·H2O, aq) | = —19 К. |
| (Na2SO4·10H2O, aq) | = —187,6 К. |
| (MnSO4, aq) | = 137,9 К. |
| (MnSO4·H2O, aq) | = 77,3 К. |
| (MnSO4·4H2O, aq) | = 20 К. |
| (МnSО 4·5H2 O, аq) | = —0,4 К. |
| (Na2CrO4, aq) | = 22 К. |
| (Na2CrO4·4H2O, aq) | = —76 К. |
| (Na2CrO4·10H2O, aq) | = —158 К. |
| (Na2HPO4, aq) | = 56 К. |
| (Na2HPO4·2H2 O, аq) | = —4 К. |
| (Na2HPO4·7H2O, aq) | = —110 К. |
| (Na2HPO4·12H2O, aq) | = —228 К. |
| (Na2CO3, aq) | = 56,4 К. |
| (Na2CO3·H2O, aq) | = 25,1 К. |
| (Na2CO3·10H2O, aq) | = —161,6 К. |
| (Zn(C2H3O2)2, aq) | = 98 К. |
| (Zn(C2H3O2)2·H2O, aq) | = 70 К. |
| (Zn(C2H3O2)2·2H2O, aq) | = 42 К. |
Разность теплот растворения безводного вещества и его кристаллогидрата равна теплоте образования кристаллогидрата из безводного вещества и жидкой воды. Такие теплоты образования кристаллогидратов всегда положительны. Кристаллогидраты, содержащие несколько частиц воды, дают для отдельных частиц Н 2 O различные тепловые эффекты. Как показали подробные по этому вопросу исследования Томсена, лишь в редких случаях все частицы Н 2 O кристаллогидрата присоединяются с одинаковым выделением тепла для каждой. Такой случай представляет, напр., пирофосфорная соль натрия Na 4P2O7·12H2 O: каждая частица воды присоединяется с выделением 23,5 К. В случае неравенства тепловых эффектов присоединения отдельных частиц воды, наблюдаются следующие случаи. Кристаллогидраты с четным числом Н 2 O: 1) присоединение молекул воды происходит попарно с одинаковым развитием тепла для каждой молекулы в паре. Например, выделение тепла в К.
|
Na2PtCl6 |
K2Mg(SO4)2 |
K2Zn(SSO4)2 |
K2 Сu(SО 4)2 |
K2Mn(SO4)2 |
|
| I. Молекула воды |
43,2 |
49,3 |
37,3 |
53,0 |
46,5 |
| II. Молекулы воды | |||||
| III. Молекулы воды |
25,4 |
29,5 |
27,3 |
29,9 |
17,6 |
| IV. Молекулы воды | |||||
| V. Молекул воды |
27,3 |
24,3 |
34,5 |
31,8 |
— |
| VI. Молекул воды |
Сюда же относятся такие случаи, как обыкн. фосфорно-натриевая соль, Na 2HPO4·12H2 O, для которой первым двум молекулам соответствует выделение по 30,2 К., а каждой из десяти остальных — по 22,4 К. 2) Первая и вторая молекулы присоединяются с различным тепловым эффектом, остальные попарно, как в предыдущем случае:
|
SrCl2 |
Na2CO3 |
Na2SO4 |
|
|
I. |
52,6 |
33,8 |
23,6 |
|
II. |
38,0 |
22,3 |
18,7 |
|
III. |
24,6 |
21,3 |
|
|
IV. |
|||
|
V. |
23,3 |
20,8 |
|
|
VI. |
|||
|
VII. |
— |
21,2 |
|
|
VIII. |
|||
|
IX. |
— |
17,6 |
|
|
X. |
3) Неправильная группировка молекул воды.
|
SrBr2 |
CaCl2 |
BaCl2 |
MgCl2 |
|
|
I. |
61,5 |
Сумма 74,4 |
31,71 |
Сумма 209,4 |
|
II. |
38,0 |
38,3 |
||
|
II Ι. |
31,0 |
Сумма 143,1 |
— |
|
|
IV. |
— |
43,7 |
||
|
V. |
31,6 |
— |
||
|
VI. |
40,0 |
— |
32,9 |
Для кристаллогидратов с нечетным числом частиц воды правильностей не наблюдается:
|
MgSO4 |
MnSO4 |
ZnSO4 |
CuSO4 |
|
|
I. |
69,8 |
59,9 |
84,8 |
64,6 |
|
II. |
23,0 |
16,0 |
23,5 |
32,5 |
|
III. |
34,0 |
19,8 |
||
|
IV. |
17,5 |
21,8 |
||
|
V. |
21,7 |
22,0 |
21,8 |
34,1 |
|
VI. |
— |
— |
||
|
VII. |
36,6 |
— |
34,2 |
— |
Теплоты разбавления растворов твердых тел. При прибавлении к одному и тому же раствору все больших и больших количеств растворителя, тепловой эффект в громадном большинстве случаев приближается асимптотически к некоторой предельной величине, как это видно на следующих примерах:
| (ZnSO4·2OH2O, mH2O): |
пpи m = 30 + 3,2 К. |
|
80 + 3,7 К. |
|
|
180 + 3,9 К. |
|
| (Na2SO4.5OH2O, mH2O): |
при m = 50 — 6,7 К. |
|
150 — 11,3 К. |
|
|
350 — 13,8 К. |
|
|
750 — 14,8 К. |
Для едкого натра наблюдается иное, весьма странное отношение: теплота разбавления растет до некоторого максимума, после которого при дальнейшем разведении наблюдается изменение ее в обратную сторону, падение ее. Это видно из следующей таблицы Томсена:
(NaOH·nН 2 O, mН 2O) =
|
n + m |
||||||||
|
5 |
7 |
9 |
20 |
25 |
50 |
100 |
200 |
|
|
n = 3 |
21,3 К. |
28,9 К. |
30,1 К. |
32,8 К. |
32,6 К. |
31,1 К. |
30,0 К. |
29,4 К. |
|
5 |
— " |
7,6 " |
9,6 " |
11,5 " |
11,3 " |
9,8 " |
8,7 " |
8,1 " |
|
7 |
— " |
— " |
2,0 " |
3,9 " |
3,7 " |
2,2 " |
1,1 " |
0,5 " |
|
9 |
— " |
— " |
— " |
1,9 " |
1,7 " |
0,2 " |
— 0,9 " |
— 1,5 " |
|
20 |
— " |
— " |
— " |
— " |
— 0,2 " |
— 1,7 " |
— 2,8 " |
— 3,4 " |
|
25 |
— " |
— " |
— " |
— " |
— " |
— 1,5 " |
— 2,6 " |
— 3,2 " |
|
50 |
— " |
— " |
— " |
— " |
— " |
— " |
— 1,1 " |
— 1,7 " |
|
100 |
— " |
— " |
— " |
— " |
— " |
— " |
— " |
— 0,6 " |
Максимум находится около раствора NaOH·20H 2 O. Теплота разбавления растворов, содержащих менее 20Н 2 O, положительна, для растворов с 20 и более частицами воды — отрицательна.
Теплота осаждения вещества из раствора равна теплоте растворения, но с обратным знаком. При этом должно быть выполнено условие, чтобы выделяющееся тело было химически и физически тождественно с первоначально растворенным. В противном случае эти две величины будут разниться одна от другой на величину теплового эффекта превращения одного видоизменения, скажем, растворяемого, в другое, осаждаемое. Как с самостоятельной величиной приходится иметь дело с теплотой осаждения в случае труднорастворимых веществ, когда теплота растворения не может быть определена вследствие ничтожной их растворимости. В таких случаях теплотой осаждения называют тепловой эффект, сопровождающий образование осадка, напр., при двойных соляных разложениях. Часто осадки тотчас после осаждения претерпевают изменения, сопровождающиеся тепловым эффектом и тем обусловливающие разные величины теплот осаждения: тотчас после осаждения и после того, как осадок принял окончательную, более стойкую форму. Так, Бертело нашел, что при смешении растворов SrCl 2 и Na 2O3 выделяется аморфный осадок SrCO 3 с поглощением 8 К.; тотчас после осаждения осадок изменяет свое сложение, из аморфного переходит в кристаллический, результатом чего является вместо поглощения 8 К. выделение 11,2 К. При осаждении йодистого серебра из разведенного раствора AgNO 3 pacтвором KJ выделяется 231 К.; через 3—4 минуты тепловой эффект возрастает до 264 К. и затем более не изменяется. Прибавка 33 К. есть результат изменения первоначально образовавшегося осадка. Исследования Томсена показали, что для аналогичных соединений теплота осаждения увеличивается с уменьшением растворимости. Так, для галоидных соединений закиси таллия и окисей свинца и серебра растворимость уменьшается при переходе от хлористых соединений к йодистым, а теплоты осаждения имеют следующие величины:
|
ТlСl |
+ 101,0 К. |
|
ТlВr |
+ 137,5 К. |
|
TlJ |
+ 178,5 К. |
|
РbСl 2 |
+ 68,0 К. |
|
РbВr 2 |
+ 100,4 К. |
|
PbJ2 |
+ 164,4 К. |
|
AgCl |
+ 158,5 К. |
|
AgBr |
+ 201,0 К. |
|
AgJ |
+ 264,2 К. |
Теплоты аллотропических и полиморфных превращений. Переходы простого вещества из одного аллотропического видоизменения в другое, или сложного вещества в твердом состоянии из аморфного в кристаллическое, или из одной кристаллической формы в другую сопровождаются большим или меньшим тепловым эффектом в зависимости от различных запасов внутренней энергии, соответствующих различным видоизменениям одного и того же вещества. Следующая таблица дает имеющиеся относительно этого предмета числовые данные, найденные главным образом Бертело:
|
Простые тела |
|
|
Превращение |
Тепловой эффект в К. |
| Кислород в озон 3О = О 3 |
—296 |
| Сера ромбическая в призматическую |
—1,5 |
| Сера ромбическая в аморфную, нерастворимую в CS 2 |
0 при 18°; <0 при 112° |
| Сера ромбическая в аморфную, растворимую в CS 2 |
—1,6 |
| Сера ромбическая в мягкую |
—8 (непостоянное число) |
| Селен металлический в аморфный |
—57 |
| Теллур кристаллический в аморфный |
+242 |
| Фосфор белый в красный |
От +207 до —10, смотря по видоизменениям красного фосфора. |
| Мышьяк кристаллический в аморфные видоизменения |
Ок. —10 |
| Кремний кристаллический в аморфный |
—69 |
| Углерод: алмаз в графит |
—5 |
| Углерод: алмаз в уголь (древесный) |
—33,4 |
| Углерод: графит в уголь (древесный) |
—28,4 |
| Марганец из амальгамы в сплавленный |
+35 |
| Марганец из амальгамы, нагретый до красного каления в сплавленный |
+31 |
|
Сложные тела. |
|
| As2O3 кристаллический в стекловидный |
—12 |
| As2O3 кристаллический в непрозрачный |
+12 |
| Sb2O3 призматическая или аморфная в октаэдрическую |
+12 |
| Sb2S3 красная, осажденная в черную, кристаллическую |
0 |
| СаСО 3 аморфный в изв. шпат |
+14 |
| СаСО 3 аморфный в аррагонит |
+17 |
| Са 3 (РО 4)2 желатинообразный в другие видоизменения |
от 0 до —56 |
| Sr3(PO4)2 желатинообразный в другие видоизменения |
от 0 до —38 |
| SrCO3 аморфный в кристаллический |
+11 |
| Bа 3 (РО 4)2 аморфный в кристаллический |
+174 |
| МnСО 3 аморфный в кристаллический |
+16 |
| SeMn аморфный в кристаллический |
—8 |
| SeFe аморфный в кристаллический |
+8 |
| SeCo аморфный в кристаллический |
—40 |
| SeNi аморфный в кристаллический |
—48 |
| SeZn аморфный в кристаллический |
—7 |
| SeTl аморфный в кристаллический |
—61 |
| SeCd аморфный в кристаллический |
—94 |
| SePb аморфный в кристаллический |
+27 |
| CuO при низкой температуре в прокаленную |
+20 |
| HgO желтая в красную 0 |
0 |
| HgJ2 желтая в красную |
+30 |
| HgCl2 сплавленная в кристаллическую |
+8 |
| HgBr2 сплавленная в кристаллическую |
+6 |
| HgCl2·HgJ2 свежесплавленная в устойчивую форму |
+64 |
| HgS черная в киноварь |
+3 |
| AgBr осажденная в конечную устойчивую форму |
+34 |
| AgJ осажденная в конечную устойчивую форму |
+56 |
| Ag2CO2 осажденная в конечную устойчивую форму |
> +35 |
| PbCO3 осажденная в конечную устойчивую форму |
> +50 |
Теплоты образования. Выше было показано, что основной закон Т. выражается уравнением U1 = U2 + Q, где U есть внутренняя энергия. Весь запас внутренней энергии никогда не может быть определен сполна: мы можем определить только разность внутренних энергий системы в двух различных состояниях ее. Для того, чтобы возможно было численно выразить величину внутренней энергии системы в данном состоянии, принимают условно какое-либо из состояний системы за начальное (напр., для газов при 0° и 760 мм давления), и тогда числом выражается, насколько больше или меньше запас внутренней энергии системы в данном состоянии сравнительно с начальным. В Т. за такое начальное состояние принимается состояние элементов в виде простых тел при температуре, при которой совершается реакция. Тогда тепловой эффект реакции, соответствующий теплоте образования сложного вещества, равен разности внутренних энергий простых тел, вступающих в реакцию, и сложного вещества, при реакции образовавшегося. Так, уравнение:
Рb + 2J = PbJ 2 + 398 К.
обозначает, что внутренняя энергия РbJ 2 на 398 К. меньше суммы внутренних энергий Pb и 2J. Таково термодинамическое значение теплот образовании.
Теплоты образования неорганических соединений. Лишь в редких случаях теплоты образования неорганических соединений могут быть определены непосредственно; в громадном большинстве они определены косвенным путем с помощью более или менее сложной системы реакций. В следующих таблицах приведены формулы и теплоты образования главнейших неорганических соединений. Все они соответствуют температуре 18°. Это температура определений Томсена, числам которого дано преимущество перед числами других исследователей. Данные других авторов соответственно перечислены. Даны величины истинных тепловых эффектов, т. е. к наблюденным уже присчитана величина внешней работы. Единица тепла — средняя калория К. Aq при формуле вещества обозначает, что тепловой эффект соответствует теплоте образования соединения в растворе из элементов и большого количества воды: напр. HClOЗ Aq + 240К. отвечает реакции: Н+Сl+3О+Aq = Η Cl Ο 3 Aq+240К.
| Кислород. | |
| О 3 | — 296 по Бертело; |
| O3 | — 362 пo Вaн дep Мульдену; которое число более достоверно — еще неизвестно. |
| Водород. | |
| Н 2O | + 676 |
| Н 2O | + 577 при 100°, вода в виде пара. |
| H2O2 | + 445 |
| Хлор. | |
| HCl | + 220 |
| Cl2O | — 178 |
| HOClAq | + 300 |
| HClO3Aq | + 240 |
| НСlO 4 Аq | + 386 |
| НСlО 4 | + 183 |
| Бром. | |
| НВr | + 84 |
| HBrOAq | + 261 |
| HBrO3Aq | + 123 |
| Йод. | |
| HJ | — 61 |
| HJO3SAq | + 557 |
| J2O5 | + 453 |
| HJO4Aq | + 476 |
| JCl | + 58 |
| JCl3 | + 215 |
| Фтор. | |
| НF | + 386 |
| Сера. | |
| Н 2S | + 27 |
| SO2 | + 711 |
| SO3 | + 1033 |
| H2SO4 | + 1930 |
| H2S2O8Aq | + 2567 |
| H2S2O3Aq | + 1373 |
| S2Cl2 | + 143 |
| S2Br2 | + 10 |
| SO2Cl2 | + 898 |
| SOCl2 | + 498 |
| S2O5Cl2 | + 1927 |
| Селен. | |
| H2Se | — 254 |
| SeO2 | + 572 |
| H2SeO4Aq | + 1452 |
| Se2Cl2 | + 222 |
| SeCl4 | + 462 |
| Теллур. | |
| H2Te | — 350 |
| H2TeO3 | + 1449 |
| H2TeO4Aq | + 985 |
| TeCl4 | + 774 |
| Азот. | |
| NH3 | + 120 |
| N2O | — 180 |
| H2N2O2Aq | — 574 |
| HNO2Aq | + 308 |
| HNO3 | + 416 |
| N2O5 | + 131 |
| NO2 | — 20,5 |
| N2O4 | — 39 |
| NO | — 216 |
| NH3O | + 243 |
| N2H4 | — 17 |
| N2H5.OHAq | + 561 |
| HN3Aq | — 621 |
| Фосфор. | |
| Р 2O5 | + 3600 |
| H3PO4Aq | + 3056 |
| PH3 | + 43 |
| Ρ 2H | + 88 |
| ΡΗ 4J | + 222 |
| PCl3 | + 755 |
| PCl5 | + 1050 |
| POCl3 | + 1460 |
| РВr 3 | + 448 |
| POBr3 | + 1056 |
| PJ2 | + 99 |
| PJ3 | + 109 |
| Мышьяк. | |
| As2O5 | + 2194 |
| H3AsO4Aq | + 2141 |
| As2O3 | + 1547 |
| AsH3 | — 441 |
| AsCl3 | + 715 |
| AsBr3 | + 449 |
| AsJ3 | + 127 |
| Сурьма. | |
| Sb2O3 | + 1660 |
| H3SbO4 | + 2158 |
| SbH3 | — 818 |
| SbCl3 | + 914 |
| SbOCl | + 897 |
| SbCl5 | + 1049 |
| SbBr3 | + 649 |
| Sb2S3 (осажд.) | + 351 |
| Бор. | |
| В 2O3 | + 3172 |
| Н 3BO3 | + 2660 |
| ВСl 3 | + 1040 |
| Углерод (исходным веществом взят алмаз). | |
| СО 2 | + 943 |
| СО | + 263 |
| СН 4 | + 187 |
| СОСl 2 | + 529 |
| CCl4 | + 532 |
| COS | + 341 |
| CS2 | — 223 |
| Кремний. | |
| SiO2Aq | + 1779 |
| Кварц | + 2192 |
| Калий. | |
| KОН | + 1032 |
| KСl | + 1056 |
| KClO3 | + 950 |
| KСlО 4 | + 1131 |
| KBr | + 953 |
| KBrO3 | + 841 |
| KJ | + 801 |
| KJO3 | + 1245 |
| KF | + 1095 |
| K2S | + 1012 |
| KHS | + 623 |
| K2SO4 | + 3446 |
| KHSO4 | + 2775 |
| KNO3 | + 1195 |
| K2CO3 | + 2784 |
| KНСО 3 | + 2329 |
| Натрий. | |
| Na2O | + 1002 |
| NaOH | + 1019 |
| NaCl | + 976 |
| NaBr | + 858 |
| NaJ | + 691 |
| Na2S | + 870 |
| Na2SO4Aq | + 3290 |
| NaNO3 | + 3113 |
| NaH2PO4Aq | + 3638 |
| Na2HPO4Aq | + 4195 |
| Na3PO4Aq | + 4698 |
| Na2HPO4 | + 4139 |
| Na2CO3 | + 2699 |
| NaHCO3 | + 2270 |
| Аммоний. | |
| NH4Cl | + 758 |
| NH4Br | + 654 |
| NH4J | + 458 |
| (NH4)2SO4 | + 2822 |
| NH4NO3 | + 880 |
| NH4HO2 | + 649 |
| Литий. | |
| LiCl | + 938 |
| Li2SO4 | + 3342 |
| LiNO3 | + 1116 |
| Барий. | |
| BaO | + 1242 |
| Ba(OH)2 | + 2149 |
| BaO2 | + 1416 |
| BaCl2 | + 1947 |
| BaBr2 | + 1700 |
| BaS | + 983 |
| BaSO4 | + 3381 |
| Ba(NO3)2 | + 2262 |
| BaCO3 | + 2805 |
| Стронций. | |
| SrO | + 1284 |
| Sr(OH)2 | + 2145 |
| SrCl2 | + 1846 |
| SrBr2 | + 1577 |
| SrS | + 974 |
| Sr(NO3)2 | + 2198 |
| SrCO3 | + 2775 |
| Кальций. | |
| СаО | + 1310 |
| Са(ОН) 2 | + 2149 |
| CaCl2 | + 1698 |
| СаВr 2 | + 1409 |
| СaJ 2 | + 1073 |
| CaS | + 896 |
| CaSO4 | + 3184 |
| Ca(NO3)2 | + 2026 |
| CaCO3 | + 2677 |
| Магний. | |
| MgO | + 1460 |
| Mg(OH)2 | + 2173 |
| MgCl2 | + 1510 |
| MgS | + 776 |
| MgSO4 | + 3023 |
| Алюминий. | |
| Al(OH)3 | + 2970 |
| AlCl3 | + 1610 |
| AlBr3 | + 1197 |
| AlJ3 | + 704 |
| Al2S3 | + 1224 |
| Марганец. | |
| Mn(OH)2 | + 1624 |
| MnCl2 | + 1120 |
| MnSO4 | + 2499 |
| MnCO3 | + 2108 |
| KMnO4 | + 1952 |
| Железо. | |
| Fе(ОН) 2 | + 1359 |
| Fe(OH)3 | + 1970 |
| Fе 3O4 | + 2647 |
| FeCl2 | + 821 |
| FeCl3 | + 961 |
| Кобальт. | |
| Со(ОН) 2 | + 1310 |
| CoCl2 | + 765 |
| Никель. | |
| Ni(ОН) 2 | + 1284 |
| NiСl 2 | + 745 |
| Цинк. | |
| ZnO | + 853 |
| Zn(OH)2 | + 1503 |
| ZnCl2 | + 972 |
| ZnBr2 | + 760 |
| ZnJ2 | + 492 |
| ZnSO4 | + 2300 |
| Кадмий. | |
| Cd(OH)2 | + 1333 |
| CdCl2 | + 932 |
| CdBr2 | + 752 |
| CdJ2 | + 488 |
| CdCO3 | + 1792 |
| Медь. | |
| CuO | + 372 |
| CuCl2 | + 516 |
| CuBr2 | + 326 |
| CuSO4 | + 1826 |
| Сu 2O | + 408 |
| CuCl | + 329 |
| CuBr | + 250 |
| CuJ | + 163 |
| CuS | + 183 |
| Ртуть. | |
| HgO (желтая) | + 201 |
| HgCl2 | + 533 |
| HgBr2 | + 405 |
| HgJ2 | + 242 |
| HgS (осажден.) | + 48 |
| Hg2O | + 220 |
| HgCl | + 314 |
| HgBr | + 243 |
| HgJ | + 141 |
| Серебро. | |
| Ag2O | + 59 |
| AgCl | + 294 |
| AgBr | + 227 |
| AgJ | + 138 |
| Ag2S | + 33 |
| Ag2SO4 | + 1673 |
| AgNO3 | + 287 |
| Ag2O3 | + 1202 |
| Таллий. | |
| Тl 2 О | + 423 |
| ТlOН | + 570 |
| TlBr | + 413 |
| TlJ | + 302 |
| TlS | + 197 |
| Tl(OH)3 | + 1446 |
| Свинец. | |
| PbO | + 503 |
| PbO2 | + 634 |
| PbCl2 | + 828 |
| PbBr2 | + 645 |
| PbJ2 | + 398 |
| PbS | + 183 |
| PbSO4 | + 2162 |
| Pb(NO3)2 | + 1055 |
| PbCO3 | + 1669 |
| Висмут. | |
| Β i(ΟΗ)3 | + 1705 |
| BiCl3 | + 906 |
| BiOCl | + 882 |
| Олово. | |
| SnO | + 660 |
| SnCl2 | + 808 |
| SnO2 | + 1356 |
| SnCl4 | + 1273 |
| Золото. | |
| Аu(ОН) 3 | + 948 |
| AuCl3 | + 228 |
| AuCl | + 58 |
| AuBr | — 1 |
| AuJ | — 55 |
| Платина. | |
| PtCl4 | + 598 |
| H2PtCl6Aq | + 1632 |
| Pt(OH)2 | + 855 |
| Палладий. | |
| Pd(OH)4 | + 1656 |
| Pd(OH)2 | + 903 |
| PdJ2 | + 183 |
Теплоты образования органических соединений. Для всех органических соединений существует общий метод определения теплот образования из элементов посредством теплот горения. Теплоты горения до полного сгорания в углекислоту, воду и т. п. определяются в специальных приборах (см. ст. Калориметрия). Теплота образования равна разности теплот горения элементов и соединения. Так, напр., теплота горения муравьиной кислоты в газообразном состоянии равна 684 К., водорода 683 К. и алмаза 943 К. Написав это в виде уравнений:
2Н + О = Н 2 O + 683 К.
С + О 2 = СО 2 + 943 К.
Н 2CO3 + О = СO 2 + Н 2 O + 624 К.
и вычтя третье уравнение из суммы первых двух, получим:
С + 2Н + 2O = H 2CO2 + 932 К.
теплоту образования муравьиной кислоты в газообразном состоянии при постоянном давлении. Так как здесь все время приходится иметь дело с газами, то необходимо обращать особое внимание на величину внешней работы. Соответствующие поправки вводятся так, как это было указано выше. В следующей таблице даны теплоты образования при постоянном объеме, выраженные в К., главнейших представителей различных классов органических соединений. Взяты числа Бертело, Лугинина и Штомана, отнесенные к теплоте горения углерода в виде алмаза. Числа Томсена для теплот образования органических соединений не заслуживают доверия, вследствие несовершенства примененных им методов.
| Углеводороды жирного ряда. | |
| Метан СH 4 | + 187 |
| Этан C 2H6 | + 233 |
| Пропан C 3H8 | + 305 |
| Гексан н. C 6H14 | + 558 |
| Этилен С 2H4 | — 146 |
| Пропилен С 3H6 | — 94 |
| Триметилен C 3H6 | — 171 |
| Ацетилен C 2H2 | — 581 |
| Аллилен С 3H4 | — 526 |
| Диметилдиацетилен С 6H6 | — 773 |
| Углеводороды ароматического и терпенного ряда. | |
| Бензол C 6H6 | — 85 |
| Толуол C 7O8 | + 2 |
| м. Ксилол C 8H10 | + 128 |
| о. Ксилол C 8H10 | + 127 |
| п. Ксилол C 8H10 | + 127 |
| Дифенил С 12 Н 10 | — 198 |
| Дибензил С 14 Н 14 | — 123 |
| Дифенилметан С 13 Н 12 | — 197 |
| Трифенилметан С 19 Н 16 | — 424 |
| Трифенилбензол С 24 Н 18 | — 613 |
| Стирол C 8H8 | — 175 |
| Стильбен С 14 Н 12 | — 357 |
| Толан С 14 Н 10 | — 789 |
| Нафталин С 10 Н 18 | — 244 |
| Антрацен С 14 Н 10 | — 333 |
| Фенантрен С 14 Н 10 | — 325 |
| Теребентен С 10 Н 16 | + 113 |
| Камфен С 10 Н 16 | + 228 |
| Терекамфен С 10 Н 16 | + 252 |
| Борнеокамфен С 10 Н 16 | + 216 |
| Одноатомные спирты. | |
| Метиловый СН 4O | + 614 |
| Этиловый C 2H6O | + 693 |
| Пропиловый C 3H8O | + 777 |
| Изопропиловый C 3H8O | + 797 |
| Изобутиловый С 4H10 О | + 843 |
| Триметилкарбинол С 4H10 О | + 882 |
| Аллиловый C 3H6O | + 463 |
| Бензойный С 7H8O | + 392 |
| Дифенилкарбинол С 13 Н 12 О | + 200 |
| Трифенилкарбинол С 19 Н 18 О | — 38 |
| Многоатомные спирты. | |
| Этиленгликол C 2H6O | + 1117 |
| Пропиленгликол C 2H8O | + 1268 |
| Изопропиленгликол С 3H8O2 | + 1218 |
| Глицерин С 3H8O3 | + 1655 |
| Эритрит С 4 Н 10 О 4 | + 2190 |
| Маннит C 6H14O6 | + 3301 |
| Дульцит C 6H14O6 | + 3357 |
| Фенолы. | |
| фенол С 6H6 О | + 361 |
| о. Крезол C 7H8O | + 542 |
| м. Крезол C 7H8O | + 530 |
| п. Крезол C 7H8O | + 536 |
| Резорцин C 6H6O2 | + 876 |
| Гидрохинон С 6H6O2 | + 877 |
| Пирокатехин C 6H6O2 | + 858 |
| Пирогаллол C 6H6O3 | + 1545 |
| Флороглюцин С 6H6O3 | + 1533 |
| Простые эфиры. | |
| Окись этилена С 2H4O | + 238 |
| Метиловый эфир C 2H6O | + 508 |
| Этиловый эфир C 4H10O | + 694 |
| Фенилметиловый эфир C 7H8O | + 327 |
| Фенилэтиловый эфир C 8H10O | + 398 |
| Альдегиды. | |
| Уксусный альд. (пар) C 2H4O | + 505 |
| Паральдегид C 6H12O3 | + 1648 |
| Метальдегид C 6H12O3 | + 1722 |
| Валериановый альд. С 5H10 О | — 728 |
| Кротоновый альд. C 4H6O | + 407 |
| Бензойный альд. C 7H6O | + 233 |
| Коричный альд. C 9H8O | + 91 |
| Кетоны. | |
| Ацетон C 3H6O | + 654 |
| Диэтилкетон C 5H10 Ο | + 781 |
| Дипропилкетон С 7H14O | + 872 |
| Диизопропилкетон С 7H14O | + 953 |
| Ацетофенон C 8H8O | + 266 |
| Бензофенон С 13 Н 10 О | + 94 |
| Карвон С 10 Н 14 О | + 483 |
| Хинон C 6H4O2 | + 474 |
| Кислоты жирного ряда. | |
| Муравьиная СН 2O2 | + 1005 |
| Уксусная C 2H4O2 | + 1166 |
| Гликоловая С 2H4O3 | + 1588 |
| Пропионовая СЗН 6O2 | + 1221 |
| Кротоновая C 4H6O2 | + 1050 |
| Масляная C 4H8O2 | + 1293 |
| Изомасляная C 4H8O2 | + 1342 |
| Оксиизомасляная С 4H8O3 | + 1342 |
| Валериановая C 5H10O2 | + 1383 |
| Пальмитиновая С 16 Н 32 О 2 | + 2461 |
| Стеариновая С 18 Н 36 О 2 | + 2562 |
| Олеиновая С 18 Н 34 О 2 | + 1830 |
| Щавелевая C 2H2O4 | + 2056 |
| Малоновая С 3H4O4 | + 2128 |
| Янтарная C 4H6O4 | + 2272 |
| Фумаровая C 4H4O4 | + 1957 |
| Малеиновая С 4H4O | + 1864 |
| Винная C 4H6O6 | + 3213 |
| Лимонная C 6H8O7 | + 3651 |
| Кислоты ароматического ряда. | |
| Бензойная C 7H6O2 | + 934 |
| Салициловая C 7H6O3 | + 1300 |
| Фенилуксусная C 8H8O2 | + 950 |
| Коричная C 9H8O2 | + 797 |
| α-нафтойная C 11H8O2 | + 774 |
| β-нафтойная C 11H8O2 | + 816 |
| Фталевая о- C 8H6O4 | + 1861 |
| Изофталевая м- C 8H6O4 | + 1902 |
| Терефталевая п- C 8H6O4 | + 1881 |
| Дигидрофталевая C 8H8O4 | + 1849 |
| Δ 1. 4-дигидротерефталевая C 8H8O4 | + 1919 |
| Δ 1. 5-дигидротерефталевая C 8H8O4 | + 1853 |
| Δ 2. 5-дигидротерефталевая C 8H8O4 | + 1826 |
| Δ 1-тетрагидротерефталевая C 8H10O4 | + 2142 |
| Δ 2-тетрагидротерефталевая C 8H10O4 | + 2154 |
| cis-гексагидротерефталевая C 8H12O4 | + 2374 |
| trans-гексагидротерефталевая C 8H12O4 | + 2365 |
| Меллитовая C 12H6O12 | + 5468 |
| Камфарная правая C 10H16O4 | + 2414 |
| Камфарная левая C 10H16O4 | + 2462 |
| Камфарная недеятельная C 10H16O4 | + 2385 |
| Изокамфорная C 10H16O4 | + 2411 |
| Ангидриды кислот. | |
| Янтарный C 4H4O3 | + 1431 |
| Малеиновый C 4H2O3 | + 1103 |
| Пропионовый C 6H10O3 | + 1619 |
| Бензойный C 14H10O3 | + 1048 |
| Фталевый C 8H4O3 | + 1069 |
| Камфарный C 10H14O3 | + 1706 |
| Сложные эфиры. | |
| Метилмуравьинокислый C 2H4O2 | + 942 |
| Метилбензойнокислый C 8H8O2 | + 840 |
| Метил-β-нафтойнокислый C 12H10O2 | + 706 |
| Диметилуглекислый C 3H6O3 | + 1493 |
| Диметилщавелекислый C4H6O4 | + 1809 |
| Этилмуравьинокислый C 3H6O2 | + 1084 |
| Этилбензойнокислый C 9H10O2 | + 917 |
| Диэтилуглекислый C 5H10O3 | + 1728 |
| Диэтилщавелевокислый C 6H10O4 | + 1928 |
| Диэтилмалоновокислый C 7H12O4 | + 2114 |
| Диэтилянтарнокислый C 8H14O4 | + 2273 |
| Триэтиллимоннокислый C 12H20O7 | + 3584 |
| Аллилуксуснокислый C 5H8O2 | + 902 |
| Бензойнокислый пропил C 10H12O2 | + 990 |
| Бензойнокислый изобутил C 11H14O2 | + 1050 |
| Бензойнокислый амил C 12H16O2 | + 1100 |
| Бензойнокислый фенил C 13H10O2 | + 618 |
| Амины. | |
| Метиламин СН 5N | + 96 |
| Диметиламин С 2 Н 7N | + 35 |
| Триметиламин С 3 Н 9N | + 149 |
| Этиламин С 2 Н 7N | + 198 |
| Диэтиламин С 4 Н 11N | + 386 |
| Триэтиламин С 6 Н 15N | + 432 |
| Бензиламин С 7 Н 9N | — 1 |
| Анилин С 6 Н 7N | — 130 |
| о-Толуидин С 7 Н 9N | + 38 |
| м-Толуидин | + 29 |
| п-Толуидин | + 97 |
| Метиланилин С 7 Н 9N | —55 |
| Диметиланилин С 8 Н 11N | —115 |
| Азо- и нитросоединения. | |
| Фенилгидразин С 6 Н 8N2 | + 337 |
| Азобензол С 12 Н 10N2 | — 834 |
| Азоксибензол С 12 Н 10N2O | — 576 |
| Гидразобензол C 12H12N2 | — 576 |
| Азотнокислый диaзoбeнзoл C 6H5N3O3 | — 474 |
| о-Динитробензол C 6H4N2O4 | — 15 |
| м-Динитробензол | + 50 |
| п-Динитробензол | + 66 |
| 1. 3. 5-Тринитробензол C 6H3N3O6 | + 37 |
| 1. 2. 4- Тринитробензол | — 110 |
| Амиды и амидокислоты. | |
| Ацетамид C 2H5NO | + 724 |
| Пропионамид C 3H7NO | + 875 |
| Бензамид C 7H7NO | + 472 |
| Ацетанилид C 8H9NO | + 457 |
| Бензанилид C 13H11NO | + 178 |
| Мочевина CH 4N2O | + 805 |
| Гликокол C 2H5NO2 | + 1256 |
| Аланин C3H7NO2 | + 1343 |
| Саркозин C 3H7NO2 | + 1223 |
| Аллантоин C 4H6N4O3 | + 1692 |
| Аспарагин C 4H8N2O3 | + 2039 |
| Креатин C 4H9N3O2 | + 1265 |
| Лейцин C 6H13NO2 | + 1566 |
| Теобромин C 7H8N4O2 | + 881 |
| Кофеин C 8H10N4O2 | + 810 |
| Тирозин C 9H11NO З | + 1543 |
| Парабановая кислота C 3H2N2O3 | + 1383 |
| Оксалуровая кислота C 3H4N2O4 | + 2090 |
| Аспарагиновая кислота C 4H7NO4 | + 2307 |
| Гиппуровая кислота C 9H9NO3 | + 1420 |
| Мочевая кислота C 5H4N4O3 | + 1475 |
| Нитрилы. | |
| Циан C 2N2 | — 741 |
| Цианистый водород HCN | — 236 |
| Ацетонитрил C 2H3N | — 1,5 |
| Пропионитрил C 3H5N | + 78 |
| Малонитрил C 3H2N2 | — 441 |
| Бензонитрил C 7H6N | — 9 |
| Галоидопроизводные. | |
| Хлористый метил СН 3Cl | + 278 |
| Хлористый метилен (пар) СН 2Cl2 | + 312 |
| Хлороформ СНСl 3 | + 286 |
| Хлористый углерод CCl 4 | + 352 |
| Хлористый этил С 2 Н 5Cl | + 211 |
| Хлористый этилиден С 2 Н 4Cl2 | + 339 |
| Гексахлорэтан C 2Cl6 | + 568 |
| Тетрахлорэтилен C 2Cl4 | + 62 |
| Бромистый метил (пар) CH 3Br | + 171 |
| Бромистый этил (пар) C 2H5Br | + 310 |
| Йодистый этил (пар) CH 3J | + 88 |
| Углеводы. | |
| Арабиноза C 5H10O5 | + 2580 |
| Ксилоза C 5H10O5 | + 2543 |
| Фукоза C 6H12O5 | + 2658 |
| Рамноза C 6H12O5 | + 2595 |
| Лактоза C 6H12O6 | + 3194 |
| Инозит C 6H12O6 | + 3115 |
| Инозит недеятельный C 6H12O6 | + 3162 |
| Декстроза C 6H12O6 | + 3046 |
| Сорбиноза C 6H12O6 | + 3094 |
| Галактоза C 6H12O6 | + 3081 |
| Фруктоза C 6H12O6 | + 3021 |
| Глюкогептоза C 7H14O7 | + 3571 |
| Тростниковый сахар C 12H22O11 | + 5320 |
| Арабиновая кислота C 12H22O11 | + 5176 |
| Молочный сахар C 12H22O11 | + 5611 |
| Мальтоза C 12H22O11 | + 5363 |
| Трегалоза C 12H22O11 | + 5371 |
| Раффиноза C 18H32O16 | + 7699 |
| Мелецитоза C 18H34O17 | + 8220 |
| Декстрин C 6H10O5 | + 2417 |
| Инулин C 6H10O5 | + 2306 |
| Целлюлоза C 6H10O5 | + 2310 |
| Крахмал C 6H10O5 | + 2315 |
Термонейтральность и теплота нейтрализации. Явление термонейтральности было открыто Гессом в 1842 году. Сущность его состоит в том, что смешение растворов нейтральных солей сопровождается нулевым тепловым эффектам, хотя при этом, согласно закону Бертоллета, происходит распределение обоих оснований между обеими кислотами, т. е. настоящая химическая реакция: из двух взятых солей получается четыре. Отсутствие теплового эффекта, очевидно, указывает на то, что тепло, поглощаемое разложением двух солей при смешении их растворов, равно теплу, выделяемому образованием двух новых солей с перемененными кислотами и основаниями. Причиной термонейтральности Гесс считал то, что одна и та же кислота при образовании солей с разными основаниями дает одинаковые тепловые эффекты. Андрюс принимал, наоборот, именно, что величина теплового эффекта зависит только от основания, а не от кислот, образующих соли. Фавр и Зильберман дали правильное объяснение термонейтральности: причина ее — постоянство величин разниц теплот нейтрализации двух оснований с любыми кислотами и двух кислот с любыми основаниями.
Если обозначить через f(а 1b1), f(а 1b2)... теплоты нейтрализации ряда кислот а 1, а 2, а 3... и оснований b1, b2, b3 ..., то в таблице
f(a1b1) f(a1b2) f(a1b3)...
f(a2b1) f(a2b2) f(a2b3)...
f(a3b1) f(a3b2) f(a3b3)...
разница соответствующих членов двух вертикальных или горизонтальных рядов величина постоянная.
Так: f(a1b1) — f(a1b2) = f(a2b1) — f(a2b2) =...
и f(a1b1) — f(a2b1) = f(a1b2) — f(a2b2) =...
При смешении двух растворов солей a1b2 и a2b1 в растворе образуются четыре соли: a1b1, a2b2, а 1b2 и a2b1, и тепловой эффект должен быть равен нулю, чтобы удовлетворить предыдущим уравнениям:
f(a1b1) + f(a2b2) — f(a1b2) — f(a2b1) = 0.
Из явления термонейтральности следует, что тепло нейтрализации составляется из двух независимых слагаемых, из которых одно зависит только от природы кислоты, а другое только от природы основания, причем индивидуальная природа образующейся соли не влияет на тепловой эффект взаимодействия кислоты и основания. Здесь проявляется столь часто наблюдаемая для растворов солей (см. статью Растворы) слагаемость свойств, резко отличающая соли от других химических соединений, для которых величина теплового эффекта определяется именно индивидуальными свойствами образующегося соединения и о слагаемости не может быть и речи. Термонейтральность наблюдается далеко не для всех солей: имеется целый ряд исключений. Но эти последние сопровождаются всегда наличностью особых условий, и благодаря этому является возможность глубже заглянуть в природу растворов солей. Отступления от термонейтральности всегда связаны с отступлениями от нормальных свойств растворов типичных солей и объясняются именно этими последними неправильностями. Разлагаемость солей водою, образование кислых и основных солей, большие различия в величинах активности (жадности) кислот и оснований и т. п. — все это условия, нарушающие простую аддитивность свойств соляных растворов и тем обусловливающие отступления от термонейтральности. Рассмотрение этих вопросов относится к химической механике. Теплота нейтрализации, как мы видели, слагается из двух величин: одной, зависящей от природы кислоты, другой — от природы основания. Сообразно этому мы рассмотрим сперва теплоты нейтрализации различных кислот одним и тем же основанием, а затем теплоты нейтрализации различных оснований одной и тою же кислотой. Первые исследователи теплот нейтрализации думали, что большая или меньшая теплота нейтрализации может служить прямой мерой большей или меньшей силы кислоты или основания. Дальнейшие исследования показали, что кислоты с очень большой теплотой нейтрализации, как, например, плавиковая и большая часть органических кислот, слабее других кислот с меньшею теплотой нейтрализации, как азотная или соляная. Современные представления о силе кислот и оснований основаны на изучении распределения одного и того же основания между различными кислотами и кислоты между различными основаниями; распределение сопровождается тепловым эффектом, являющимся сложной функцией теплот нейтрализации, смешения разных растворов и др.; подробности об этом см. статьи Химическое сродство и Жадность кислот и оснований. Сильные одноосновные кислоты представляют простейший случай теплот нейтрализации. Теплоты нейтрализации их едким натром близки между собою, около 137 К.; дальнейшая прибавка к раствору средней соли кислоты или щелочи не дает никакого теплового эффекта. Сюда относятся:
|
НСl |
137,4 К. |
|
HBr |
137,5 К. |
|
HJ |
136,8 К. |
|
HNO3 |
136,8 К. |
|
HClO3 |
137,6 К. |
|
HBrO3 |
137,8 К. |
|
HJO3 |
138,1 К. |
|
HClO4 |
143,5 К. |
Кислоты плавиковая и фосфорноватистая дают большие теплоты нейтрализации, 162,7 К. для первой и 151,6 К. для второй, не дают теплового эффекта при прибавлении избытка NaOH, но, наоборот, поглощают тепло при прибавлении кислоты к средней соли. Для органических кислот теплоты нейтрализации равны: муравьиная 134,5 К., уксусная 134,0 К., пропионовая 134,8 К., монохлороуксусная 142,8 К., дихлороуксусная 148,3 К. и трихлороуксусная 139,2 К. Слабые кислоты, соли которых в растворе отчасти разложены водой на кислоту и основания, имеют теплоты нейтрализации гораздо меньше. Так, для хлорноватистой найдено 98,4 К., для синильной 27,7 К.
Двуосновные кислоты делятся по их теплотам нейтрализации на две группы. К первой группе относятся кислоты, для которых оба эквивалента щелочи при нейтрализации выделяют одинаковые количества тепла. Для таких кислот действие кислоты на среднюю соль не сопровождается тепловым эффектом: кислая соль образуется из средней и кислоты без поглощения и без выделения тепла. Сюда относятся кислоты: платинохлористоводородная H 2Pt2Cl6 с теплотой нейтрализации 136 К. на каждый эквивалент NaOH, кремнефтористоводородная H 2SiF6 и дитионовая Н 2S2O6. Ко второй группе относятся кислоты с различными теплотами нейтрализации для первого и второго атомов водорода:
|
I экв. NaHO |
II экв. NaHO |
|
| Н 2 SО 4 |
147,5 К. |
166,3 К. |
| Н 2 SеО 4 |
147,6 К. |
156,3 К. |
| C2H2O4 |
138,5 К. |
144,3 К. |
| Яблочная к. |
130,4 К. |
131,3 К. |
| Винная к. |
124,4 К. |
128,7 К. |
| H2CrO4 |
131,4 К. |
115,8 К. |
| H2SO3 |
158,7 К. |
131,0 К. |
| Н 2 SеО 3 |
147,7 К. |
122 5 К. |
| Η 3P Ο 3 |
148,3 К. |
136,2 К. |
| Η 2C Ο 3 |
110,0 К. |
92,0 К. |
Из этой таблицы видно, что для кислот Н 2 SО 4, Н 2 SеО 4, C2H2O4, яблочной и винной кислые соли образуются из средних с поглощением тепла; наоборот, для остальных кислот — с выделением. Так же, как для слабых одноосновных кислот, и угольная кислота, средние соли которой имеют щелочную реакцию, т. е. разлагаются водой, имеет незначительную теплоту нейтрализации: в растворе соль не образуется нацело, а остаются еще свободная кислота и щелочь.
Теплоты нейтрализации оснований имеют следующие величины. Щелочи и щелочные земли с серной и соляной кислотами
|
H2SO4 |
2HCl |
|
| 2LiOH |
313 К. |
277 К. |
| 2NaOH |
314 К. |
275 К. |
| 2KOH |
313 К. |
275 К. |
| 2TlOH |
311 К. |
443 К. |
| Ba(OH)2 |
369 К. |
278 К. |
| Sr(OH)2 |
307 К. |
276 К. |
| Ca(OH)2 |
311 К. |
279 К. |
| NH3 |
282 К. |
122 К. |
Все они имеют очень близкие величины, кроме тех случаев, когда получаются труднорастворимые соли ТlСl и BaSO 4, и аммиака, представляющего слабое основание. Для других оснований получены следующие числа:
|
H2SO4 |
2HCl |
|
| Mg(OH)2 |
311 К. |
277 К. |
| Mn(OH)2 |
266 К. |
230 К. |
| Ni(OH)2 |
263 К. |
226 К. |
| Co(OH)2 |
247 К. |
211 К. |
| Fe(OH)2 |
249 К. |
214 К. |
| Cd(OH)2 |
238 К. |
203 К. |
| Zn(OH)2 |
235 К. |
199 К. |
| Cu(OH)2 |
184 К. |
149 К. |
| 2Al(OH)3 |
3 × 211 К. |
3 × 186 К. |
| 2Cr(OH)3 |
3 × 164 К. |
3 × 137 К. |
| 2Fе(ОН) 3 |
3 × 112 К. |
3 × 112 К. |
Эти числа не могут быть сравниваемы непосредственно с теплотами нейтрализации щелочей и щелочных земель, так как они заключают неизвестные еще теплоты растворения нерастворимых водных окисей. Но и так видно, что основания, дающие мало прочные, разлагаемые водой соли, как Al(HO) 3, Fe(OH)3, Cr(OH)8, имеют низшие теплоты нейтрализации, чем остальные.
В заключение необходимо указать, как смотрят современные теории растворов на термонейтральность и теплоты нейтрализации. Электролитическая, или физико-механическая (см. Растворы), теория растворов предполагает, что соли, сильные кислоты и основания в растворах вполне диссоциированы на свои ионы, напр. NaCl на Na + и Cl — , HNO3 на Н + и NO 3— , NaOH на Na + и ОН — . При смешении растворов солей или раствора соли и сильной кислоты все четыре иона продолжают сосуществовать в растворе рядом, и тепловой эффект смешения должен быть равен нулю, так как никакой реакции, собственно говоря, не происходит: (К + + Cl— ) + (Na+ + NO3— ) = К + + Cl— + Na+ + NO3— . Это и есть причина термонейтральности. При нейтрализации сильной кислоты сильным основанием происходит образование воды из ионов ОН — и Н +: (Н + + Cl— ) + (Na+ + ОН — ) = Na+ + Cl— + H2 O. Тепловой эффект в 137 К., сопровождающий нейтрализацию всех сильных одноосновных кислот и сильных оснований, и есть тепло, выделяющееся при образовании частицы воды из ионов Н + и ОН — . Для кислот слабых, малодиссоциированных, соли которых, между тем, диссоциированы почти нацело, теплота нейтрализации есть сумма 137 К. и теплоты электролитической диссоциации кислоты. Таким образом вычислены теплоты электролитической диссоциации для следующих кислот:
| Уксусная кислота | + 3 К. |
| Дихлороуксусная | — 11,3 К. |
| Фосфорная | — 11,3 К. |
| Плавиковая | — 25,7 К. |
Для двуосновных кислот явления усложняются ступенчатой диссоциацией, образованием кислых солей, разлагаемостью последних водою и т. д., и благодаря этому окончательный анализ фактов не удается выполнить. Физико-химическая теория растворов еще не дала своего объяснении термонейтральности и постоянства величины 137 К. для разных кислот и оснований.
Приложения второго закона термодинамики. Второй закон термодинамики определяет направление, в котором протекает какой-либо начавшийся процесс — вопрос, которого не касается вовсе закон сохранения энергии. Например, уравнение, вытекающее из приложения I-го закона термодинамики:
{Н 2 } + {0} = (Н 2 O) + 684 К.
означает, что газообразные водород и кислород, образуя при постоянном давлении жидкую воду и сохраняя при этом первоначальную температуру, отдают окружающей среде количество тепла, измеряемое 684 К., и наоборот, то же количество тепла отнимается от окружающей среды при разложении воды в тех же условиях. Но вопрос о том, разлагается ли на самом деле вода или смесь газов дает воду и может ли реакция идти сама по себе в одном из этих направлений, — остается открытым. Второй закон термодинамики указывает, что, если в окружающей среде не происходит никаких других изменений, процесс идет только в одном из указанных двух направлений. При изменении условий окружающей среды процесс может быть выполнен в обоих направлениях: различными средствами можно и воду разложить на ее составные части и из этих последних получить воду. В свою очередь, II закон термодинамики не касается вопроса, начинается ли процесс в указанном законом направлении сам собою или для этого требуется какой-нибудь толчок (напр., искра); не касается он также того, как протекает процесс во времени. Вышесказанным указывается и ограничивается приложение второго закона термодинамики в термохимии.
II закон термодинамики отличает обратимые и необратимые процессы. Процесс обратим, когда система может его пройти в одном направлении и в противоположном; в обоих случаях система проходит через одни и те же состояния, но порядок, в котором эти состояния следуют одно за другим, в одном случае один, в другом — противоположный. Процесс необратим, если он может проходить только в одном направлении. Если произошел необратимый процесс, то уже ни при каких условиях и никакими средствами не может быть восстановлено первоначальное состояние всех тел, подвергающихся изменениям во время самого процесса или при попытках произвести его в обратном направлении. Из этого видно различие начального и конечного состояний системы при различных процессах: при обратимом процессе возможен переход от одного к другому и обратно, при необратимом — очевидно, конечное состояние системы обладает некоторым особым свойством, отличающим его от первоначального и делающим невозможным обратное направление, процесса. II закон термодинамики и знакомит нас с этими особыми свойствами различных состояний систем и, обратно, раз известны два состояния системы, указывает, протекает ли процесс в направлении от первого к второму или наоборот. Для этой цели необходима полная характеристика состояний системы, необходимо знать не только химический состав, но физические условия, в которых находится система, как то: агрегатное состояние, температуру, давление, электрический потенциал и т. д. Задача, преследуемая приложением II закона термодинамики, та же, что и у принципа максимальной работы Бертело: определение направления химической реакции. Но между тем, как Бертело принимает во внимание только химическую энергию, считая, что другие факторы, названные им посторонними энергиями, лишь нарушают закономерное течение реакций, модифицируя их и даже давая им обратное требуемому принципом направление, II закон термодинамики не знает этих отличий, а считается со всеми факторами, со всеми условиями, под влиянием которых система находится. Свойством, обусловливающим обратимость или необратимость процесса, является энтропия системы, обозначаемая обыкновенно буквой S. Процесс обратим, если энтропии системы не меняется, т. е. если величина энтропии Sa начального состоянии системы равна величине Sb конечного состояния. Следовательно, условие обратимости процесса: Sa = Sb и dS = 0. Процесс необратим, когда энтропия системы увеличивается: Sa < Sb и dS > 0. Для всех возможных процессов: dS > 0.
Измеряется величина изменения энтропии системы отношением количества тепла, полученного системой от окружающей среды, и абсолютной температуры, при которой состоялась передача тепла: dS = dQ/T.
Все процессы, действительно имеющие место в природе, необратимы: при всяком процессе сумма энтропий всех участвующих в нем тел (веществ, подвергающихся химическому превращению, и окружающей среды, являющейся источником механической и тепловой энергий) — увеличивается. При этом для отдельных частей системы энтропия может оставаться неизменной или даже уменьшаться; но общая сумма всех изменений энтропии — величина всегда положительная. Рассмотрим теперь, каким образом на основании предыдущего определяются условия, необходимые для того, чтобы какое-нибудь химическое превращение могло совершиться. Возьмем систему из каких-либо тел при условии, что в самой системе и в окружающей среде господствуют постоянная температура T и постоянное давление р. При всех возможных превращениях, согласно закону сохранения энергии, тепло, полученное системой от окружающей среды, равно:
dQ = dU + dr = dU + pdV
где: T — внутренняя энергия системы, r — внешняя работа при превращении, приложенная к системе, а V — объем системы. Согласно второму закону, всякое изменение, могущее произойти, сопровождается увеличением всей энтропии, т. е. суммы S — энтропии системы, подвергающейся химической реакции, и s0 — энтропии окружающей среды dS + dS0 > 0.
А так как dS0 = dQ/T, то после соответствующих подстановок:
dS — dU/T — (pdV)/(AT) > 0 ...(1)
где А есть термический эквивалент механической работы. Неравенство (1) заключает только величины, относящиеся к самой системе, и выражает в общей форме условие для возможности превращения независимо от какого-либо ограничения по отношению к температуре, давлению или поглощенному системой теплу; оно есть наиболее общая форма для приложений II закона термодинамики к Т., сделанных различными авторами. Левая часть неравенства не есть полный дифференциал какой-нибудь величины; поэтому выражение не может быть сполна интегрировано, т. е. оно не может быть применено для конечного изменения состояния системы. Для такого применения необходимо знать некоторые внешние условия, дающие возможность интегрировать выражение. Наиболее замечательные случаи, позволяющие применить II закон для любого конечного превращения системы, следующие. 1) При постоянном объеме V (dV = 0) и постоянной энергии U (dU = 0) — энтропия S системы увеличивается (Гиббс). 2) При постоянном объеме V и постоянной энтропии S (dS = 0) — энергия U системы уменьшается (Гиббс). 3) При постоянном объеме V и постоянной температуре Т увеличивается величина S = U/T, или, что то же: величина U — TS уменьшается (Гельмгольц). Величина U — TS называется свободной энергией системы. 4) При постоянной температуре Т и постоянном давлении p увеличивается величина S — U/T — (pV)/(TA) или, что то же, величина U — TS + (pV)/A уменьшается (Дюгем). Величина U — TS + (pV)/A называется термодинамическим потенциалом системы.
Таковы условия, которым должно удовлетворять превращение системы, действительно имеющее место в природе. Сравнение этих условий с принципом максимальной работы Бертело указывает, почему этот неверный в своем основании принцип иногда дает верные результаты. По этому принципу, при отсутствии внешней работы (dV = 0) и постоянной температуре тепловой эффект реакции должен быть величиной положительной. Так как в этом случае по закону сохранения энергии тепловой эффект равен изменению энергии U системы, то различие между принципом максимальной работы и II законом термодинамики состоит в том, что по первому должна уменьшаться вся энергия U, а по второму — свободная энергия U — TS системы. Поэтому, когда член TS сравнительно с U мал, например при низких температурах, оба принципа ведут к одинаковым результатам. При больших значениях S (в газах и растворах), наоборот, различие значительно, и принцип Бертело будет давать неверные выводы.
В частных случаях определение возможного направления химического превращения сводится к определению изменения свободной энергии и термодинамического потенциала системы тел, участвующих в превращении. Особенный интерес представляет свободная энергия. Из неравенства (1) видно, что dU — TdS > —(pdV)/A, внешняя работа, произведенная системой (при выводе (1) + (pdV)/A обозначало работу, произведенную внешней средой, т. е. работу, приложенную к системе), меньше уменьшения свободной энергии системы. При обратимом (идеальном) процессе внешняя работа была бы равна уменьшению свободной энергии, т. е. изменение свободной энергии есть предельный максимум внешней работы превращения. Эта максимальная работа химического превращения и принимается за меру химического средства, обусловливающего превращение. Методы определения величины химического сродства основаны на определении равновесия между реагирующими телами и на определении электровозбудительной силы соответствующих гальванических комбинаций. Описание методов и применений их к частным случаям должно искать в статьях Химическое сродство и Химические равновесия. Здесь в виде примера мы приведем несколько гальванических комбинаций, для которых определены изменение свободной энергии системы и тепловой эффект совершающегося в системе химического превращения.
|
Комбинация |
Уменьшение свободной энтропии |
Тепловой эффект |
|
Сu, Cu(C 2H3O2)2 aq. |
10842 cal. |
8766 cal. |
|
Pb, Pb(C2H3O2)2 + 100H2O |
||
|
Ag, AgCl |
23453 cal. |
26023 cal. |
|
Zn, ZnCl + 100H2O |
||
|
Ag, AgBr |
19138 cal. |
19882 cal. |
|
Zn, ZnBr2 + 25H2O |
||
|
Hg, HgCl·KCl aq. |
7566 cal. |
—3280 cal. |
|
Hg, Hg2O·KOH aq. |
Из этих данных видно, что уменьшение свободной энергии системы может быть и больше и меньше теплового эффекта реакции, равного уменьшению внутренней энергии системы. Особенно интересна последняя комбинация. В ней происходит реакция, выражаемая уравнением: HgCl + KOH = ½ (Hg2O) + ½(H2 O) + КСl. Реакция эта идет с поглощением тепла, и поэтому по принципу максимальной работы Бертело она не должна была бы иметь место. На самом деле она совершается, что вполне согласно с требованиями II закона термодинамики, так как при этом уменьшается свободная энергия системы.
Рассмотрев условия возможности химического превращения, рассмотрим условия отсутствия превращения, т. е. термохимические условия существования химического равновесия. Система находится в равновесии, если при данных условиях температуры, давления и т. д. никакое превращение в ней не может иметь места. Неравенство (1) выражает условие возможности превращения, поэтому, обратно, мы будем иметь равновесие, если в системе при любом превращении:
dS — dU/T — (pdV)/(AT) меньше или равно 0 ...(2)
Последнее выражение есть общая форма условий равновесия и, как и неравенство (1), не может быть применено непосредственно. В частных случаях оно применяется следующим образом. Система находится в равновесии, если любое превращение: 1) при постоянном объеме и постоянной энергии системы — уменьшает или оставляет неизменной ее энтропию; 2) при постоянном объеме и постоянной энтропии системы — увеличивает или оставляет неизменной ее энергию; 3) при постоянном объеме и постоянной температуре системы — увеличивает или оставляет неизменной ее свободную энергию и 4) при постоянной температуре и постоянном давлении — увеличивает или оставляет неизменным термодинамический потенциал системы. Подробности приложения этих выводов к частным случаям химического равновесия различных систем, также к случаям нарушения равновесия при изменении условий, в которых находится система, должно искать в статье Химические равновесия.
В заключение необходимо указать, что далеко не всякая реакция, требуемая II-м законом термодинамики, начинается сама собою. В большом числе случаев превращению препятствуют какие-то сопротивления, подобные трению при механических явлениях, названные Гиббсом пассивными сопротивлениями. В таких случаях для того, чтобы реакция началась, требуется некоторый толчок, как, напр., искра, подъем температуры, удар (см. Химическая реакция); раз начавшееся превращение идет уже дальше само и в ходе своем подчиняется вполне II закону. Наличность пассивных сопротивлений обусловливает образование так назыв. пассивных, или ложных, равновесий, само собою разумеется, не подчиняющихся II закону термодинамики. Сущность пассивных сопротивлений еще совершенно неясна, между тем считаться с ними приходится постоянно, и на это необходимо обращать внимание при всяких применениях II закона термодинамики к химическим явлениям.
Руководства по Т. Кроме соответствующих отделов в курсах общей химии, как то: Ostwald, "Lehrbuch der allgemeinen Chemie" (т. II: "Chemische Energie", 1893); Nernst, "Theoretische Chemie" (3 изд., 1900), можно указать на следующие книги: Berthelot, "Essai de m écanique chimique fondé e sur la thermochimie" (2 т., 1879); Thomson, "Therm o chemische Untersuchungen" (4 т., 1882—86); Naumann, "Thermochemie" (1882); Jahn, "Die Grundsä tze der Thermochemie" (1892, есть русский перев. "Основания термохимии", 1893); Лугинин, "Описание различных методов определения теплот горения органических соединений" (1894); Berthelot, "Thermochimie. Donn ées et lois numériques" (т. Ι: "Les lois numé riques", т. II: "Les donn ées expé rimentales", 1897); Gibbs, переводы: "Thermodynamische Studien" (1892) и "Equilibre des syst èmes chimiques" (1899); Planck, "Vorlesungen über Thermodynamik" (1897); Duhem, "Introduction à la mécanique c himique" (1893). Сводки числовых данных, кроме вышеуказанных сочинений Ostwald'a, Berthelot, Thomsen'a и Лугинина, имеются в Biedermannes "Chemiker-Kalender" и Landolt und B örnstein, "Physikalisch-chemische Tabellen" (1894).
E. Бирон.