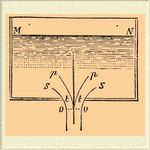
— Если резервуар, наполненный жидкостью, имеет отверстие в дне или в одной из боковых стенок, то жидкость будет вытекать из этого резервуара со скоростью тем большею, чем выше стоит уровень жидкости над отверстием; скорость истечения из некоторого отверстия будет постоянною, коль скоро высота уровня жидкости в резервуаре будет каким-либо приспособлением удерживаема постоянною. Вся жидкость в сосуде будет находиться в движении при истечении через отверстие, потому что всякий вытекший слой должен заменяться новым, опустившимся на место первого, и через каждое воображаемое сечение сосуда будет проходить в каждую единицу времени постоянное количество жидкости с постоянною в элементе поверхности скоростью и по одному направлению. Далее увидим, что направления скоростей движения жидкостей через различные части некоторого сечения могут быть не параллельны между собою. Торичелли (ученик Галилея) показал, что скорость истечения жидкости через отверстие в дне сосуда в воздух будет равна скорости, которую приобрело бы твердое тело, свободно падающее с высоты, равной высоте уровня жидкости в сосуде над уровнем дна, в котором имеется отверстие. Если высота уровня над отверстием будет обозначена через h, ускорение силы тяжести (см. Тяжесть) через g и скорость истечения жидкости через v, то v = √(2gh). В этом заключается теорема Торичелли. Подобно тому, как скорость падения тел не зависит от их массы при одинаковых прочих обстоятельствах, так и скорость истечения жидкостей не зависит от их плотности: вода и ртуть, налитые до одной и той же высоты в двух сосудах, вытекают из отверстия в дне с одинаковою скоростью. Если жидкость вытекает через отверстие, сделанное в боковой стенке сосуда, то скорость истечения будет по-прежнему соответствовать теореме Торичелли, причем h формулы будет высота уровня над отверстием, но скорость направлена горизонтально. Твердые тела, брошенные горизонтально, описывают вследствие их притяжения землею параболу; подобно тому и струя воды, вытекающая из бокового отверстия сосуда, получает вид параболы, измерением координат которой можно убедиться в верности теоремы Торичелли. Но, определяя количество воды, вытекающей через отверстие определенных размеров, и сравнивая это количество с вычисленным посредством умножения площади отверстия на скорость истечения, найденную по теореме Торичелли, находят, что действительно вытекшее количество жидкости составляет только 0,62 теоретически вычисленного количества. Это разногласие происходит от того, что при выводе теоремы не были приняты в соображение некоторые побочные обстоятельства, изменяющие вид вытекающей струи и ее поперечное сечение. Через отверстие в дне сосуда проходят не только те частицы воды, которые находятся на вертикальных линиях над отверстием, но и частицы, лежащие по сторонам, как это показано на чертеже, и скорости их направлены не вертикально, а наклонно, вследствие чего выходящая из отверстия струя принимает коническую форму.

На некотором расстоянии от отверстия струя в оо получает наибольшее сжатие и затем становится цилиндрическою. Поперечное сечение в оо составляет 0,62 поперечного сечения отверстия в tt, и вследствие этого при расчете количества вытекающей жидкости надо вводить в вычисление только 0,62 площади отверстия в дне сосуда. Если в отверстие будет вставлена короткая коническая трубка, формой подобная струе до ее сжатия, то, принимая за отверстие истечения поперечное сечение трубки на ее конце, получаем именно такое количество истекшей воды, какое по Торичеллиевой теореме должно быть для этого отверстия и соответственной высоты жидкости, и только трение жидкости о стенки такой трубки может несколько уменьшить количество вытекающей жидкости.

Цилиндрическая трубка уменьшает истекающее количество; насадочные трубки других форм производят еще большие отступления от правила Торичелли, которые трудно предвидеть или объяснить из теории. Кроме сжатия струи, обнаруживаются еще, как было замечено, трение жидкости о стенки труб и, кроме того, так называемое внутреннее трение (см. Трение жидкости), вследствие которого Т. жидкости по волосным трубкам происходит по законам сравнительно простым и подлежащим теоретическому определению (см. там же).

Строение истекающей струи. Савар показал (Savart, "Annales de chim. et de phys.", т. III), что струя, вытекающая из отверстия в дне сосуда, после сжатия не падает сплошным цилиндром, но представляет быстро следующие одни за другими утолщения и сжатия, а на некотором расстоянии от отверстия вниз разделяется на капли сфероидальные, большей или меньшей величины, и эллипсоидальные, растянутые то по направлению струи, то перпендикулярно ему. Впоследствии Магнус повторил и разнообразил эти опыты, изменяя и форму отверстия, через которое вытекала струя (щелеобразное, две пересекающиеся щели, квадратное). Эти капли не могут быть видны раздельно просто глазом, так как очень быстро следуют одна за другой. Чтобы видеть их, Савар и Магнус употребляли один и тот же, в сущности, прием. В опытах Магнуса служил вертикальный быстро вращающийся (стробоскопический) кружок, в котором были вырезаны щели по направлению радиусов. При достаточной быстроте вращения кружка каждая щель перемещалась на свою ширину в 1/15000 (и менее) секунды, поэтому, глядя чрез щель, приходившую в вертикальное положение, можно было получать оптическое впечатление, длившееся сказанный малый промежуток, в который части струи казались неподвижными. Этот разрыв струи на капли можно объяснить неустойчивостью формы длинного жидкого цилиндра, который стремится разделиться на сфероидальные капли (см. Тела жидк.). Струя, направленная согнутой трубкой вверх, вытекая из сосуда, бьет фонтаном, форма которого может быть изменена посредством твердых тел (пластинок, трубок), помещенных на пути струи (см. Фонтаны).

Ф. П.

Оглавление