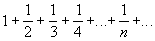
Гармонический ряд, числовой ряд
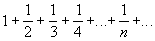
Каждый член Г. р. (начиная со 2-го) является гармоническим средним между двумя соседними (отсюда название — Г. р.). Члены Г. р. стремятся к нулю, однако Г. р. расходится (Г. Лейбниц, 1673). Сумма n первых членов Г. р. имеет следующее асимптотическое выражение (Л. Эйлер, 1740):
Sn = ln n +С+ en,
где С = 0,577215... — Эйлера постоянная, а en ® 0 при n ® ¥.