
Градусные измерения, высокоточные астрономические и геодезические измерения, выполняемые на земной поверхности для определения фигуры и размеров Земли. Современные Г. и. представляют астрономо-геодезические сети, служащие для обоснования топографических съёмок (см. Топография).
Геометрические основы Г. и. сложились в глубокой древности, когда возникло учение о шарообразности Земли и появилась практическая необходимость в определении радиуса земного шара для нужд астрономии, геодезии, географии и картографии. Первоначально Г. и. заключались в измерении линейной длины S дуги меридиана между двумя точками А и В, а также в измерениях в этих точках зенитного расстояния z (см. Небесные координаты) какого-нибудь небесного светила s в меридиане (рис. 1). Путём сопоставления линейной длины S дуги меридиана и соответствующего ей угла при центре Земли, равного разности широт конечных точек этой дуги и определяемого по формуле:
j2 - j1 = z2 - z1,
определялась длина D дуги земного меридиана:

откуда и возникло понятие об измерении градуса земной окружности или о Г. и. Этим же способом определялся и радиус R земного шара по формуле:
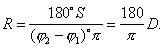
Первое в истории определение радиуса земного шара методом Г. и. было произведено жившим в Египте греческим учёным Эратосфеном около 250 до н. э. Зная, что в полдень в дни летнего солнцестояния Солнце в Сиене (ныне Асуан) освещает дно глубоких колодцев, т. е. находится в зените, а в Александрии отклоняется от зенита на 1/50 часть окружности, он определил, что измеряемое в центре Земли угловое расстояние между этими городами равно 7°12'. Линейное же расстояние между теми же городами, считая их лежащими на одном и том же меридиане, он определил по времени и скорости движения торговых караванов и принял равным 5 тыс. египетских стадий. Отсюда он нашёл, что радиус земного шара равен 39 790 стадий, т. е. 6311 км.
Одно из последующих Г. и. было произведено араб. учёными в 827 по приказу багдадского халифа Мамуна на равнине между рр. Тигром и Евфратом под широтой около 36° и основывалось на определении линейной дуги меридиана путём непосредственных измерений на местности и соответствующего ей угла в центре Земли по измерениям меридианных высот одних и тех же звёзд в её конечных точках. Это Г. и. показало, что длина дуги меридиана в один градус равна 112 км, т. е. дало для своего времени достаточно точный результат.
После изобретения голландским учёным В. Снеллиусом в 1615—17 метода триангуляции появилась возможность измерять дуги меридианов и параллелей любой длины. Применив этот метод, французский учёный Ж. Пикар в 1669—70 произвёл Г. и. по дуге меридиана от Парижа до Амьена. Для измерения углов триангуляции он впервые применил геодезические инструменты со зрительными трубами, снабженными сеткой нитей.
Во 2-й половине 17 в. обнаружились некоторые факты и явления, которые вызвали новые научные взгляды на форму Земли как планеты, изменившие задачи Г. и. Так, французский астроном Ж. Рише обнаружил, что в Кайенне, расположенной в Южной Америке, вблизи экватора, часы с маятником, выверенные в Париже, отстают на 21/2 мин в сутки и что для исправления их хода необходимо укоротить маятник на 3 мм. Аналогичный факт установил и английский астроном Э. Галлей на о. Св. Елены в 1677. Объясняя эти факты, исходя из закона всемирного тяготения, И. Ньютон в 1680 высказал мысль, что Земля не шар, а несколько сплюснута в направлении оси вращения и имеет вид сфероида. Предполагая, что все частицы массы Земли находятся в состоянии взаимного притяжения, Ньютон теоретически определил сжатие земного сфероида и получил величину 1/230. Голландский физик Х. Гюйгенс, предполагая, что массы Земли притягиваются только к её центру, в 1690 также определил сжатие земного сфероида и нашёл величину 1/576. В 1691 из непосредственных наблюдений было открыто сжатие планеты Юпитер и тем же самым получено наглядное доказательство возможной сфероидичности планет Солнечной системы.
В связи с возникновением точки зрения о том, что Земля имеет форму сфероида, который в простейшем случае является эллипсоидом вращения, задача Г. и. уже состояла в определении радиуса экватора а и полярного радиуса b Земли (рис. 2) или радиуса экватора и сжатия а земного эллипсоида, т. е. величины
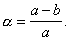
Длина дуги S меридиана на эллипсоиде вращения и широты j1 и j2 её конечных точек связаны между собой уравнением.

Если длину дуги меридиана определить из геодезических измерений, например методом триангуляции, а широты её конечных точек — из астрономических наблюдений, то в приведённом уравнении останутся два неизвестных а и а, характеризующих размеры земного эллипсоида. Поэтому для определения этих неизвестных в принципе достаточно выполнить Г. и. по двум дугам меридиана в различных географических широтах. Но в действительности для этой цели используются Г. и. по многочисленным дугам меридианов и параллелей.
Чтобы впервые определить размеры земного сфероида, т. е. доказать сплюснутость Земли в направлении её оси вращения и обоснованность закона всемирного тяготения, который ещё вызывал много споров, французские учёные Ж. Кассини, Ж. Маральди и Ф. Лаир с 1684 по 1718 выполнили Г. и. по меридиану от Парижа на север до Дюнкерка и на юг до Перпиньяна. Однако это Г. и. не только не подтвердило теоретических выводов о сплюснутости Земли в направлении оси вращения, оно показало, наоборот, что она вытянута в этом направлении. Ошибочность этого вывода можно было объяснить ошибками астрономических и геодезических измерений. Но тогда это было ещё непонятно и поэтому вызвало новые споры о справедливости закона всемирного тяготения.
Для разрешения возникших споров Парижская академия наук организовала две экспедиции по Г. и. в сильно различающихся широтах, одна из которых была направлена в Перу — к экватору, а другая в Лапландию — к Полярному кругу. Перуанская экспедиция под руководством П. Бугера при участии Ш. Кондамина и Л. Годена работала с 1735 по 1742 и измерила дугу меридиана длиной около 3°. Лапландская экспедиция под руководством П. Мопертюи при участии А. Клеро и шведского физика А. Цельсия (автора температурной шкалы) работала в 1736—37 и измерила дугу меридиана всего лишь около 1°. Результаты работ этих экспедиций и Г. и. Кассини во Франции окончательно доказали как сплюснутость Земли, так и обоснованность закона всемирного тяготения и имели огромное значение для развития геодезии и др. наук.
С 1792 по 1797 по распоряжению революционного Законодательного собрания Франции в разгар Великой французской революции было произведено значительное для своего времени Г. и. от Дюнкерка до Барселоны. Это Г. и. производилось под руководством Ж. Деламбра и П. Мешена и послужило в своё время основой для установления длины метра, как одной десятимиллионной части четверти дуги земного меридиана.
С начала 19 в. астрономо-геодезические работы по программе Г. и. стали проводиться во многих странах в целях топографического изучения и картографирования их территорий. С разработкой методов и изобретением приборов для определения разностей долгот стали развиваться Г. и. и вдоль земных параллелей. К настоящему времени Г. и. произведены во всех странах Европы. Начатые в 1800 английскими геодезистами астрономо-геодезические работы в странах Индостана постепенно превратились в Г. и. и охватили значительные территории этих стран. Предпринятые в 30-х гг. 19 в. астрономо-геодезические работы позднее приобрели характер Г. и. в США. Они связаны ныне (2-я пол. 20 в.) с аналогичными работами в Канаде и Мексике, а также в некоторых странах Южной Америки. В 1883 английскими геодезистами было начато в Африке Г. и. от мыса Доброй Надежды до Каира, которое завершилось вскоре после 2-й мировой войны. В середине 20 в. начались работы по Г. и. в Китае, Австралии и др. странах. Начатые в конце 20-х гг. 20 в. астрономо-геодезические работы в СССР привели к современным Г. и. на обширных пространствах Европы и Азии.
В России Г. и. были начаты в 1816 К. И. Теинером в западных пограничных районах и В. Я. Струве в прибалтийских губерниях. Развитие этих работ завершилось измерением дуги меридиана от устья Дуная до берегов Северного Ледовитого океана длиной около 25°20' по широте. В 19 веке в России были произведены и другие астрономо-геодезические работы, которые позднее были заменены новыми.
По мере накопления материалов Г. и. с начала 19 в. были произведены различные определения размеров земного эллипсоида. К середине 19 в. в этих определениях обнаружились значительные расхождения, которые не могли быть объяснены ошибками Г. и. Пытаясь объяснить эти разногласия, русский геодезист Ф. Ф. Шуберт в 1859 высказал мысль о возможной трёхосности Земли и впервые определил размеры земного эллипсоида с тремя неравными осями. Но представление Земли в виде трёхосного эллипсоида не устранило противоречий в результатах различных Г. и. Отсюда возникло понимание, что Земля имеет сложный вид, и её фигура, по предложению нем. физика И. Листинга в 1873, была названа геоидом. С тех пор стали считать, что задача Г. и. состоит в определении размеров земного сфероида, наиболее правильно представляющего фигуру геоида, и отступлений геоида от этого сфероида. Но оказалось, что изучение фигуры геоида требует данных о внутреннем строении Земли и связано со значительными трудностями. Чтобы избежать их, сов. геодезист М. С. Молоденский в 1945 разработал теории и методы определения фигуры физической поверхности и внешнего гравитационного поля Земли.
В СССР были проведены новые Г. и. и связанные с ними гравиметрические работы. Широкое развитие получили также исследования по определению фигуры, размеров и гравитационного поля Земли. В 1940 Ф. Н. Красовский и А. А. Изотов получили весьма важные данные о размерах земного эллипсоида, который под названием эллипсоида Красовского теперь применяется в геодезических работах СССР и др. социалистических стран (см. Красовского эллипсоид).
В настоящее время собственно Г. и. используются преимущественно только для определения размеров Земли. Характеристики же фигуры Земли, а также её гравитационного поля определяют по результатам измерений силы тяжести (см. Гравиметрия) и наблюдений движения искусственных спутников Земли (ИСЗ) и дальних космических ракет (см. Спутниковая геодезия). При одновременном же определении фигуры, размеров и гравитационного поля Земли используют совместно всю совокупность данных Г. и., измерений силы тяжести и наблюдений движения спутников.
Данные о фигуре, размерах и гравитационном поле Земли имеют большое значение для астрономии, геодезии, картографии и др. отраслей знания. Они входят в состав астрономических и геодезических постоянных и широко используются для расчётов по запуску ИСЗ и дальних космических ракет.
Лит.: Струве В. Я., Дуга меридиана в 25° 20' между Дунаем и Ледовитым морем, т. 1—2, СПБ, 1861; Витковский В. В., Практическая геодезия, 2 изд., СПБ., 1911; Деламбр Ж. и Мешен П., Основы метрической десятичной системы или измерение дуги меридиана, заключённого между параллелями Дюнкерка и Барселоны, пер. с франц., М. — Л., 1926; Михайлов А. А., Курс гравиметрии и теории фигуры Земли, 2 изд., М., 1939; Красовский Ф. Н., Руководство по высшей геодезии, ч. 2, М., 1942; Изотов А. А., Форма и размеры Земли по современным данным, «Тр. Центрального научно-исследовательского института геодезии, аэросъемки и картографии», 1950, в. 73; Молоденский М. С., Юркина М. И. и Еремеев В. Ф., Методы изучения внешнего гравитационного поля и фигуры Земли, там же, 1960, в. 131; Куликов К. А., Новая система астрономических постоянных, М., 1969.
А. А. Изотов.

Рис. 2 к ст. Градусные измерения.

Рис. 1 к ст. Градусные измерения.