Дезарга теорема, теорема проективной геометрии, установленная французским математиком Ж. Дезаргом. Д. т. утверждает (рис.), что если соответствующие стороны двух треугольников пересекаются в точках Р, Q, R, лежащих на одной прямой, то прямые, соединяющие соответствующие вершины, пересекаются в одной точке О. Справедлива и обратная теорема: если прямые, соединяющие соответствующие вершины двух треугольников, проходят через одну точку, то точки Р, Q, R пересечения соответствующих сторон этих треугольников лежат на одной прямой. Содержание Д. т. относится к взаимному расположению прямых на плоскости и не связано с измерениями. Однако, как установил Д. Гильберт, эта теорема не может быть доказана в геометрии на плоскости без привлечения метрических аксиом (существуют так называемые «недезарговы» геометрии на плоскости, в которых выполняются все проективные аксиомы, но Д. т. не имеет места). Поэтому при аксиоматическом построении проективной геометрии на плоскости условие Д. т. принимается в качестве аксиомы.
Э. Г. Позняк.
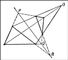
Рис. к ст. Дезарга теорема.