
Действующих масс закон, один из основных законов физической химии; устанавливает зависимость скорости химической реакции от концентраций реагирующих веществ и соотношение между концентрациями (или активностями) продуктов реакции и исходных веществ в состоянии химического равновесия. Норвежские учёные К. Гульдберг и П. Вааге, сформулировавшие Д. м. з. в 1864—67, назвали «действующей массой» вещества его количество в единице объёма, т. е. концентрацию, отсюда — наименование закона.
Если в идеальной газовой смеси или идеальном жидком растворе происходит реакция:
аА + а'А' = bB + b'B' (1)
(А, А' и т.д. — вещества, а, а' и т.д. — стехиометрические коэффициенты), то, согласно Д. м. з., скорость реакции в прямом направлении:
r+ = k+ [A] a [A'] a' (2)
Здесь [А] — концентрация вещества А и т.д., k+ — константа скорости реакции (в прямом направлении), k+ зависит от температуры, а в случае жидкого раствора — также и от давления; последняя зависимость существенна лишь при высоких давлениях. Вид уравнения (2) определяется тем, что необходимым условием элементарного акта реакции является столкновение молекул исходных веществ, т. е. их встреча в некотором малом объёме (порядка размера молекул). Вероятность найти в данный момент в данном малом объёме молекулу А пропорциональна [А]; вероятность найти в нём одновременно а молекул А и а' молекул А' по теореме о вероятности сложного события пропорциональна [А] a [А'] a'. Число столкновений молекул исходных веществ в единичном объёме за единичное время пропорционально этой величине. Определённая доля этих столкновений приводит к реакции. Отсюда вытекает уравнение (2). Мономолекулярные реакции требуют особого рассмотрения.
r- = k- [B] b [B'] b'. (3)
Если реакция обратима, т. е. протекает одновременно в противоположных направлениях, то наблюдаемая скорость реакции r = r+ – r-. При r+ = r- осуществляется химическое равновесие. Тогда, согласно уравнениям (2) и (3),

где К = k+/k- — константа равновесия. Для газовых реакций обычно применяют равноценное уравнение
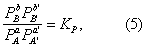
где PA — парциальное давление вещества А и т.д.
Уравнения (2) и (3) применимы к простой (одностадийной) реакции и к отдельным стадиям сложной реакции, но не к сложной реакции в целом. Уравнения (4) и (5), выражающие Д. м. з. для равновесия, справедливы и в случае сложной реакции.
Общим условием равновесия по отношению к реакции (1), приложимость которого не ограничена идеальными системами, является уравнение

в котором [А] — активность вещества А и т.д. Уравнение (6) выводится из принципов термодинамики. С помощью Д. м. з. для равновесия вычисляют максимально достижимые степени превращения при обратимых реакциях. В число последних входят важные промышленные процессы — синтез аммиака, окисление сернистого газа и многие другие. На основе Д. м. з. для скоростей реакций получают кинетические уравнения, применяемые при расчёте химической аппаратуры.
Лит. см. при ст. Кинетика химическая и Термодинамика химическая.