Информация в кибернетике. Естественнонаучное понимание И. основано на двух определениях этого понятия, предназначенных для различных целей (для информации теории, иначе называемой статистической теорией связи, и теории статистических оценок). К ним можно присоединить и третье (находящееся в стадии изучения), связанное с понятием сложности алгоритмов.

  Центральное положение понятия И. в кибернетике объясняется тем, что кибернетика (ограничивая и уточняя интуитивное представление об И.) изучает машины и живые организмы с точки зрения их способности воспринимать определённую И., сохранять её в «памяти», передавать по «каналам связи» и перерабатывать её в «сигналы», направляющие их деятельность в соответствующую сторону.

 В некоторых случаях возможность сравнения различных групп данных по содержащейся в них И. столь же естественна, как возможность сравнения плоских фигур по их «площади»; независимо от способа измерения площадей можно сказать, что фигура A имеет не большую площадь, чем B, если A может быть целиком помещена в В (сравни примеры 1—3 ниже). Более глубокий факт — возможность выразить площадь числом и на этой основе сравнить между собой фигуры произвольной формы — является результатом развитой математической теории. Подобно этому, фундаментальным результатом теории И. является утверждение о том, что в определённых весьма широких условиях можно пренебречь качественными особенностями И. и выразить её количество числом. Только этим числом определяются возможности передачи И. по каналам связи и её хранения в запоминающих устройствах.

  Пример 1. В классической механике знание положения и скорости частицы, движущейся в силовом поле, в данный момент времени даёт И. о её положении в любой будущий момент времени, притом полную в том смысле, что это положение может быть предсказано точно. Знание энергии частицы даёт И., но, очевидно, неполную.

  Пример 2. Равенство

a = b                                                                (1)

даёт И. относительно вещественных переменных a и b. Равенство

a² = b²                                                                                                                            (2)

даёт меньшую И. [так как из (1) следует (2), но эти равенства не равносильны]. Наконец, равенство

a³ = b³                                                              (3)

равносильное (1), даёт ту же И., то есть (1) и (3) — это различные формы задания одной и той же И.

  Пример 3. Результаты произведённых с ошибками независимых измерений какой-либо физической величины дают И. о её точном значении. Увеличение числа наблюдений увеличивает эту И.

  Пример 3 а. Среднее арифметическое результатов наблюдений также содержит некоторую И. относительно рассматриваемой величины. Как показывает математическая статистика, в случае нормального распределения вероятностей ошибок с известной дисперсией среднее арифметическое содержит всю И.

  Пример 4. Пусть результатом некоторого измерения является случайная величина X. При передаче по некоторому каналу связи X искажается, в результате чего на приёмном конце получают величину Y = X + q, где q не зависит от X (в смысле теории вероятностей). «Выход» Y даёт И. о «входе» X; причём естественно ожидать, что эта И. тем меньше, чем больше дисперсия случайной ошибки q.

  В каждом из приведённых примеров данные сравнивались по большей или меньшей полноте содержащейся в них И. В примерах 1—3 смысл такого сравнения ясен и сводится к анализу равносильности или неравносильности некоторых соотношений. В примерах 3 а и 4 этот смысл требует уточнения. Это уточнение даётся, соответственно, математической статистикой и теорией И. (для которых эти примеры являются типичными).

  В основе теории информации лежит предложенный в 1948 американским учёным К. Шенноном способ измерения количества И., содержащейся в одном случайном объекте (событии, величине, функции и т. п.) относительно другого случайного объекта. Этот способ приводит к выражению количества И. числом. Положение можно лучше объяснить в простейшей обстановке, когда рассматриваемые случайные объекты являются случайными величинами, принимающими лишь конечное число значений. Пусть X — случайная величина, принимающая значения x₁, x₂,..., x_n с вероятностями p₁, p₂,..., p_n, а Y — случайная величина, принимающая значения y₁, y₂,..., y_m с вероятностями q₁, q₂,..., q_m. Тогда И. I (X,Y) относительно Y, содержащаяся в X, определяется формулой

где p_ij — вероятность совмещения событий X = x_i и Y = y_j и логарифмы берутся по основанию 2. И. I (X, Y) обладает рядом свойств, которые естественно требовать от меры количества И. Так, всегда I (X, Y) ³ 0 и равенство I (X, Y) = 0 возможно тогда и только тогда, когда p_ij = p_iq_j при всех i и j, т. е. когда случайные величины X и Y независимы. Далее, всегда I (X, Y) £ I (Y, Y) и равенство возможно только в случае, когда Y есть функция от X (например, Y = X² и т. д.). Кроме того, имеет место равенство I (X, Y) = I (Y, X).

  Величина

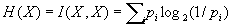
носит название энтропии случайной величины X. Понятие энтропии относится к числу основных понятий теории И. Количество И. и энтропия связаны соотношением

I (X, Y) = H (X) + H (Y) — H (X, Y),                              (5)

где H (X, Y) — энтропия пары (X, Y), т. е.

Величина энтропии указывает среднее число двоичных знаков (см. Двоичные единицы), необходимое для различения (или записи) возможных значений случайной величины (подробнее см. Кодирование, Энтропия). Это обстоятельство позволяет понять роль количества И. (4) при «хранении» И. в запоминающих устройствах. Если случайные величины X и Y независимы, то для записи значения X требуется в среднем H (X) двоичных знаков, для значения Y требуется H (Y) двоичных знаков, а для пары (X, Y) требуется Н (Х) + H (Y) двоичных знаков. Если же случайные величины X и Y зависимы, то среднее число двоичных знаков, необходимое для записи пары (X, Y), оказывается меньшим суммы Н (Х) + H (Y), так как

H (X, Y) = H (X) + H (Y) — I (X, Y).

  С помощью значительно более глубоких теорем выясняется роль количества И. (4) в вопросах передачи И. по каналам связи. Основная информационная характеристика каналов, так называемая пропускная способность (или ёмкость), определяется через понятие «И.» (подробнее см. Канал).

  Если X и Y имеют совместную плотность p(x, y), то

где буквами р и q обозначены плотности вероятности Х и Y соответственно. При этом энтропии Н (X) и Н (Y) не существуют, но имеет место формула, аналогичная (5),

I (X, Y) = h (X) + h (Y) — h (X, Y),                                           (7)

где

дифференциальная энтропия X [h (Y) и h (X, Y) определяется подобным же образом].

  Пример 5. Пусть в условиях примера 4 случайные величины X и q имеют нормальное распределение вероятностей с нулевыми средними значениями и дисперсиями, равными соответственно s²_х и s²_q. Тогда, как можно подсчитать по формулам (6) или (7):

Таким образом, количество И. в «принятом сигнале» Y относительно «переданного сигнала» X стремится к нулю при возрастании уровня «помех» q (т. е. при s²_q ® ¥) и неограниченно возрастает при исчезающе малом влиянии «помех» (т. е. при s²_q ® 0).

  Особенный интерес для теории связи представляет случай, когда в обстановке примеров 4 и 5 случайные величины X и Y заменяются случайными функциями (или, как говорят, случайными процессами) X (t) и Y (t), которые описывают изменение некоторой величины на входе и на выходе передающего устройства. Количество И. в Y (t) относительно X (t) при заданном уровне помех («шумов», по акустической терминологии) q(t) может служить критерием качества самого этого устройства (см. Сигнал, Шеннона теорема).

  В задачах математической статистики также пользуются понятием И. (сравни примеры 3 и 3а). Однако как по своему формальному определению, так и по своему назначению оно отличается от вышеприведённого (из теории И.). Статистика имеет дело с большим числом результатов наблюдений и заменяет обычно их полное перечисление указанием некоторых сводных характеристик. Иногда при такой замене происходит потеря И., но при некоторых условиях сводные характеристики содержат всю И., содержащуюся в полных данных (разъяснение смысла этого высказывания даётся в конце примера 6). Понятие И. в статистике было введено английским статистиком Р. Фишером в 1921.

  Пример 6. Пусть X₁, X₂, ..., X_n, — результаты n независимых наблюдений некоторой величины, распределённые по нормальному закону с плотностью вероятности

где параметры a и s² (среднее и дисперсия) неизвестны и должны быть оценены по результатам наблюдений. Достаточными статистиками (т. е. функциями от результатов наблюдении, содержащими всю И. о неизвестных параметрах) в этом примере являются среднее арифметическое

и так называемая эмпирическая дисперсия

Если параметр s² известен, то достаточной статистикой будет только X (сравни пример 3 а выше).

  Смысл выражения «вся И.» может быть пояснён следующим образом. Пусть имеется какая-либо функция неизвестных параметров j = j (a, s²) и пусть

j* = j*(X₁, X₂, ..., X_n)

— какая-либо её оценка, лишённая систематической ошибки. Пусть качество оценки (её точность) измеряется (как это обычно делается в задачах математической статистики) дисперсией разности j* — j. Тогда существует другая оценка j**, зависящая не от отдельных величин X_i, а только от сводных характеристик X и s², не худшая (в смысле упомянутого критерия), чем j*. Р. Фишером была предложена также мера (среднего) количества И. относительно неизвестного параметра, содержащейся в одном наблюдении. Смысл этого понятия раскрывается в теории статистических оценок.

  Лит.: Крамер Г., Математические методы статистики, пер. с англ., М., 1948; Ван-дер-Варден Б. Л., Математическая статистика, пер. с нем., М., 1960; Кульбак С., Теория информации и статистика, пер. с англ., М., 1967.

  Ю. В. Прохоров.

Оглавление