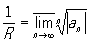
Круг сходимости степенного ряда
a0+a1(z-z0)+a2(z-z0)2+… (*)
круг |z—z0| < R в плоскости комплексного переменного z, обладающий тем свойством, что внутри него ряд (*) сходится, а вне соответствующего замкнутого круга — расходится (в точках окружности |z—z0| = R ряд может как сходиться, так и расходиться). Каждый степенной ряд или сходится на всей плоскости (при любых z), или имеет К. с. конечного радиуса R, или сходится только при z = z0. Внутри К. с. ряд (*) сходится к некоторой аналитической функции. Число R называется радиусом сходимости ряда (*) и определяется по формуле Коши — Адамара:
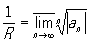
Если z0 = x0 — действительное число, то часть действительной оси Ox, лежащая внутри К. с., называется интервалом сходимости.