
Логарифмическая функция, функция, обратная к показательной функции. Л. ф. обозначается
y = lnx; (1)
её значение y, соответствующее значению аргумента х, называется натуральным логарифмом числа х. В силу определения соотношение (1) равносильно
х = еу (2)
(е — неперово число). Т. к. ey > 0 при любом действительном у, то Л. ф. определена только при х > 0. В более общем смысле Л. ф. называют функцию
y = logaX,
где а > 0 (а ¹ 1) — произвольное основание логарифмов. Однако в математическом анализе особое значение имеет функция InX; функция logaX приводится к ней по формуле:
logax = MInX,
где М = 1/In а. Л. ф. — одна из основных элементарных функций; её график (рис. 1) носит название логарифмики. Основные свойства Л. ф. вытекают из соответствующих свойств показательной функции и логарифмов; например, Л. ф. удовлетворяет функциональному уравнению
Inx+lny = lnxy.
Для - 1 < х , 1 справедливо разложение Л. ф. в степенной ряд:
ln(1 + x) = x 
Многие интегралы выражаются через Л. ф.; например
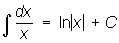 ,
,
 .
.
Л. ф. постоянно встречается в математическом анализе и его приложениях.
Л. ф. была хорошо известна математикам 17 в. Впервые зависимость между переменными величинами, выражаемая Л. ф., рассматривалась Дж. Непером (1614). Он представил зависимость между числами и их логарифмами с помощью двух точек, движущихся по параллельным прямым (рис. 2). Одна из них (У) движется равномерно, исходя из С, а другая (X), начиная движение из А, перемещается со скоростью, пропорциональной её расстоянию до В. Если положить СУ = у, ХВ = х, то, согласно этому определению, dx/dy = - kx, откуда 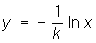 .
.
Л. ф. на комплексной плоскости является многозначной (бесконечнозначной) функцией, определённой при всех значениях аргумента z ¹ 0 обозначается Lnz. Однозначная ветвь этой функции, определяемая как
Inz = In½z½+ i arg z,
где arg z — аргумент комплексного числа z, носит название главного значения Л. ф. Имеем
Lnz = lnz + 2kpi, k = 0, ±1, ±2, ...
Все значения Л. ф. для отрицательных: действительных z являются комплексными числами. Первая удовлетворительная теория Л. ф. в комплексной плоскости была дана Л. Эйлером (1749), который исходил из определения
 .
.

Рис. 1 к ст. Логарифмическая функция.

Рис. 2 к ст. Логарифмическая функция.