;Матричные игры, понятие игр теории. М. и. — игры, в которых участвуют два игрока (I и II) с противоположными интересами, причём каждый игрок имеет конечное число чистых стратегий. Если игрок I имеет m стратегий, а игрок II — n стратегий, то игра может быть задана (m ´ n)-maтрицей А = ||aij||, где aij есть выигрыш игрока I, если он выберет стратегию i (i = -1, ..., m), а игрок II — стратегию j (j = 1, ..., n). Следуя общим принципам поведения в антагонистических играх (частным случаем которых являются М. и.), игрок I стремится выбрать такую стратегию i0, на которой достигается
;
игрок II стремится выбрать стратегию jo, на которой достигается
;
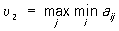Если u1 = u2, то пара (i0, j0) составляет седловую точку игры, то есть выполняется двойное неравенство
; i = 1, …, m; j = 1, …, n.
Число 
называется значением игры; стратегии i0, j0 называются оптимальным и чистыми стратегиями игроков I и II соответственно. Если u1 ¹ u2, то всегда u1 < u2; в этом случае в игре седловой точки нет, а оптимальные стратегии игроков следует искать среди их смешанных стратегий (то есть вероятностных распределений на множестве чистых стратегий). В этом случае игроки оперируют уже с математическими ожиданиями выигрышей.
Основная теорема теории М. и. (теорема Неймана о минимаксе) утверждает, что в любой М. и. существуют оптимальные смешанные стратегии х*, у*, на которых достигаемые «минимаксы» равны (общее их значение есть значение игры). Например, игра с матрицей 
имеет седловую точку при i0 = 2, j0 = 1, а значение игры равно 2; игра с матрицей 
не имеет седловой точки. Для неё оптимальные смешанные стратегии суть х* = (3/4, 1/4), y* = (1/2, 1/2); значение игры равно 1/2.
Для фактического нахождения оптимальных смешанных стратегий чаще всего используют возможность сведения М. и. к задачам линейного программирования. Можно использовать так называемый итеративный метод Брауна — Робинсон, состоящий в последовательном фиктивном «разыгрывании» данной игры с выбором игроками в каждой данной партии своих чистых стратегий, наилучших против накопленных к этому моменту стратегий оппонента. Игры, в которых один из игроков имеет только две стратегии, просто решить графически.
М. и. могут служить математическими моделями многих простейших конфликтных ситуаций из области экономики, математической статистики, военного дела, биологии. Нередко в качестве одного из игроков рассматривают «природу», под которой понимается вся совокупность внешних обстоятельств, неизвестных принимающему решения лицу (другому игроку).
Лит.: Матричные игры. [Сборник переводов], под редакцией Н. Н. Воробьева, М., 1961; Нейман Дж. фон, Моргенштерн О., Теория игр и экономическое поведение, перевод с английского, М., 1970; Оуэн Г., Теория игр, перевод с английского, М., 1971.
А. А. Корбут.