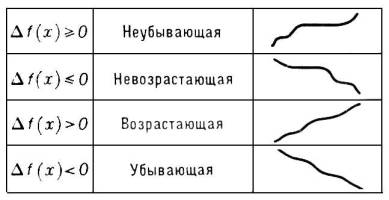
Монотонная функция (от греч. monótonos — однотонный), функция, приращения которой Df(x) = f(x’) — f(x) при Dx = x’ — x > 0 не меняют знака, т. е. либо всегда неотрицательны, либо всегда неположительны. Выражаясь не совсем точно, М. ф. — это функции, меняющиеся в одном и том же направлении. Различные типы М. ф. представлены на прилагаемой табл.:

Например, функция у = x³ является возрастающей функцией. Если функция f(x) имеет в каждой точке производную f’(x), которая неотрицательна и обращается в нуль лишь в конечном числе отдельных точек, то f(x) — возрастающая функция. Аналогично, если f’(x) £ 0 и обращается в нуль только в конечном числе точек, то f(x) — убывающая функция.

  Условие монотонности может выполняться как для всех х, так и для х из некоторого интервала (или отрезка). В этом последнем случае функцию называют монотонной на этом интервале (или отрезке). Например, функция  возрастает на отрезке [ — 1, 0] и убывает на отрезке [0, + 1].

  М. ф. представляют собой один из простейших классов функций и постоянно встречаются в математическом анализе и теории функций. Если f(x) — М. ф., то для любого x₀ существуют пределы

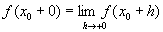
  и

Таблица к ст. Монотонная функция.

Оглавление БСЭ