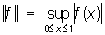Нормированное кольцо, важное понятие функционального анализа, значительно расширившее область его приложений. Элементы Н. к. являются одновременно и точками некоторого геометрического образования — полного нормированного пространства, и элементами некоторого алгебраического образования — кольца, в котором определено ещё умножение на числа (причём алгебраические операции непрерывны по норме). Примерами Н. к. могут служить: кольцо С всех непрерывных функций на отрезке [0,1] с обычными алгебраическими операциями и нормой 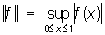, кольцо L₁ всех абсолютно интегрируемых на прямой функций, в котором умножение определено как свёртывание:

  , ;

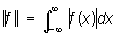  кольцо матриц n-го порядка; кольцо ограниченных операторов гильбертова пространства — кольцо операторов, и т.д. Наиболее разработана теория коммутативных Н. к. (т. е. Н. к., в которых умножение перестановочно: ху = ух), созданная И. М. Гельфандом.

  Наряду с термином «Н. к.» употребляется термин «банахова алгебра».

  Лит.: Наймарк М. А., Нормированные кольца, М., 1956.

Оглавление БСЭ