Параллельное перенесение, обобщение понятия параллельного переноса на пространства более сложной структуры, чем евклидовы (например, так называемые пространства афинной связности и, в частности, римановы пространства). П. п. позволяет сравнивать геометрические образы, относящиеся к различным точкам пространства.

  На поверхности S в трёхмерном евклидовом пространстве (являющейся двумерным римановым пространством) П. п. определяется следующим образом. Пусть g — кривая на поверхности S, А и В— концы g; S — развёртывающаяся поверхность, которая является огибающей семейства касательных плоскостей, построенных в точках кривой g (см. рис.). Тогда П. п. вектора а, заданного в касательной плоскости П_А в точке А, называется параллельный перенос этого вектора по развёрнутой на плоскость поверхности S с последующим приложением S к g. На рис. вектор а* представляет собой результат П. п. вектора а по поверхности S вдоль g. П. п. можно рассматривать как некоторое линейное преобразование касательной плоскости П_А в точке А в касательную плоскость Пв в точке В. Такое преобразование может быть описано с помощью формул, зависящих от Кристоффеля символов. Эти формулы обобщаются на римановы пространства большей размерности и на пространства аффинной связности; символы Кристоффеля соответственно могут быть вычислены с помощью метрического тензора (см. Риманова геометрия) или задаются как исходные величины теории.

  Вообще говоря, результат П. п. вектора зависит не только от исходного вектора, начальной и конечной точек перенесения, но и от выбора самого пути перенесения.

  Если результат П. п. вектора не зависит от выбора пути, то пространство (по крайней мере, в достаточно малой окрестности) является аффинным или евклидовым и понятие П. п. совпадает с понятием параллельного переноса. См. также Связность и лит. при этой статье.

  Д. Д. Соколов.

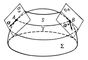
Рис. к ст. Параллельное перенесение .

Оглавление БСЭ