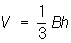 ,
,Пирамида (от греч. pyramís, родительный падеж pyramídos), многогранник, одной из граней которого служит многоугольник (основание П., которое, в частности, может быть треугольником), а остальные грани (боковые) суть треугольники с общей вершиной (вершина П.) (см. рис. 1, 2). В зависимости от числа боковых граней П. делятся на треугольные, четырёхугольные и т.д. Отрезок перпендикуляра, опущенного из вершины П. на плоскость её основания (а также его длина), называется высотой П. Объём П. вычисляется по формуле
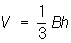 ,
,
где В — площадь основания, h — высота. П. называется правильной (см. рис. 2), если в основании её лежит правильный многоугольник и высота П. проходит через центр основания. Боковые грани правильной П. суть равные между собой равнобедренные треугольники; высота каждого из этих треугольников называется апофемой правильной П. (апофема основания П. служит проекцией апофемы П. на плоскость основания). Рассекая П. плоскостью, параллельной её основанию, получим две части: П., подобную данной, и так называемую усечённую П.

Рис. 1 (слева) и рис. 2 (справа) к ст. Пирамида.