Плотность вероятности случайной величины X, функция р(х), такая, что при любых a и b вероятность неравенства а < Х < b равна

.

  Например, если Х имеет нормальное распределение, то

.

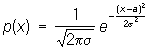  Если П. в. p(x) непрерывна, то при достаточно малых dx вероятность неравенства x < X < x + dx приближённо равна p(x)dx. П. в. всегда удовлетворяет условиям

.

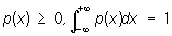  Аналогично определяют П. в. p(x₁,...,x_s) для нескольких случайных величин X₁, X₂, ..., X_s (т. н. совместную П. в.): при любых a_i, b_i вероятность одновременного выполнения неравенств a₁ < X_i < b₁, . . ., a_s < X_s < b_s равна

.

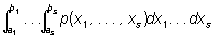  Если существует совместная П. в. X₁, Х₂, ..., X_s, то для независимости этих величин необходимо и достаточно. чтобы совместная П. в. была произведением П. в. отдельных величин X_i, i = 1, 2, . . ., s.

Оглавление БСЭ