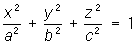— эллипсоиды,Поверхности второго порядка, поверхности, декартовы прямоугольные координаты точек которых удовлетворяют алгебраическому уравнению 2-й степени:
a11x2 + a22y2 + a33z2 + 2a12xy + 2a23yz + 2a13xz + 2a14x + 2a24y + 2a34z + a44 = 0 (*)
Уравнение (*) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую П. в. п. В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат к одному из 17 приведённых ниже канонических видов, каждому из которых соответствует определённый класс П. в. п. Среди них выделяют пять основных типов поверхностей. Именно,
1) эллипсоиды
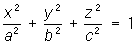— эллипсоиды,
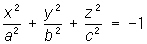— мнимые эллипсоиды;
2) гиперболоиды:
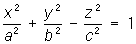— однополостные гиперболоиды,
— двуполостные гиперболоиды;
3) параболоиды (p > 0, q > 0):
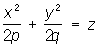— эллиптические параболоиды,
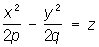— гиперболические параболоиды;
4) конусы второго порядка:
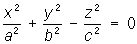— конусы,
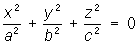— мнимые конусы;
5) цилиндры второго порядка:
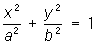— эллиптические цилиндры,
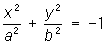— мнимые эллиптические цилиндры,
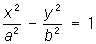— гиперболические цилиндры,
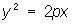— параболические цилиндры.
Перечисленные П. в. п. относятся к т. н. нераспадающимся П. в. п.; распадающиеся П. в. п.:
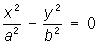— пары пересекающихся плоскостей,
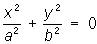— пары мнимых пересекающихся плоскостей,
х2 = а2 — пары параллельных плоскостей,
х2 = —а2 — пары мнимых параллельных плоскостей,
х2 = 0 — пары совпадающих плоскостей.
При исследовании общего уравнения П. в. п. важное значение имеют т. н. основные инварианты — выражения, составленные из коэффициентов уравнения (*) и не меняющиеся при параллельном переносе и повороте системы координат. Например, если
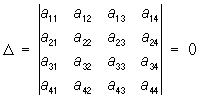(aij = ajii),
то уравнение (*) определяет вырожденные П. в. п.: конусы и цилиндры второго порядка и распадающиеся П. в. п.; если определитель
,
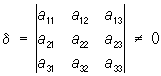то поверхность имеет единственный центр симметрии (центр П. в. п.) и называется центральной поверхностью. Если d = 0, то поверхность либо не имеет центра, либо имеет бесконечно много центров.
Для П. в. п. установлена аффинная и проективная классификация. Две П. в. п. считают принадлежащими одному аффинному классу, если они могут быть переведены друг в друга некоторым аффинным преобразованием (аналогично определяются проективные классы П. в. п.). Каждому аффинному классу соответствует один из 17 канонических видов уравнения П. в. п. Проективные преобразования позволяют установить связь между различными аффинными классами П. в. п. Это объясняется тем, что при этих преобразованиях исчезает особая роль бесконечно удалённых элементов пространства. Например, эллипсоиды и двуполостные гиперболоиды, различные с аффинной точки зрения, принадлежат одному проективному классу П. в. п.
Лит.: Александров П. С., Лекции по аналитической геометрии..., М., 1968; Ильин В. А., Позняк Э. Г., Аналитическая геометрия, 2 изд., М., 1971; Ефимов Н. В., Квадратичные формы и матрицы, 5 изд., М., 1972.
А. Б. Иванов.