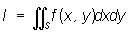
Повторный интеграл, понятие интегрального исчисления. Вычисление двойного интеграла
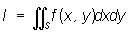
(см. Кратный интеграл) от функции f (x, у) по области S, ограниченной прямыми х = а, х = b и кривыми y = j1(x), у = j2(х), при некоторых условиях относительно функций f (x, у), j1(x), j2(х), производится по формуле:
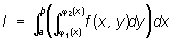 ,
,
где при вычислении внутреннего интеграла х считается постоянным. Таким образом, вычисление двойного интеграла сводится к двум вычислениям обычных интегралов, или, как говорят, к П. и. Геометрически сведение двойного интеграла к П. и. означает возможность вычисления объёма цилиндроида как путём разбиения его на элементарные столбики, так и путём разбиения его на элементарные слои, параллельные плоскости yOz. При некоторых условиях на функцию f (x, у) область S в П. и. можно изменить порядок интегрирования (то есть сначала интегрировать по х, а потом по у). Аналогично определяется П. и. в случае функций большего числа переменных.
Лит. см. при ст. Интегральное исчисление.