Автофазировка, явление, обеспечивающее ускорение электронов, протонов, альфа-частиц, многозарядных ионов до высоких энергий (от нескольких Мэв до сотен Гэв) в большинстве ускорителей заряженных частиц; открыто советским физиком В. И. Векслером в 1944 и независимо от него американским физиком Э. Макмилланом в 1945. Принципиальную роль это явление сыграло в повышении предела достижимых энергий в циклических ускорителях.

  В циклических ускорителях частицы совершают движение по орбитам в специальной вакуумной камере, помещенной в магнитное поле, и многократно проходят через ускоряющие электроды. Ускорение частиц происходит под действием высокочастотного электрического поля, приложенного к ускоряющим электродам. Для непрерывного ускорения частиц необходимо, чтобы в моменты ускорения направления движения частицы и электрического поля совпадали; для этого нужно обеспечить синхронизм (резонанс) между движением частиц и изменением электрического поля. Если амплитуда разности потенциалов между электродами равна V₀, то приобретаемая частицей с зарядом е энергия DЕ при каждом прохождении через ускоряющий промежуток равна DЕ = eV₀cosj, где (j — фаза электрического поля в момент прохождения частицы, отсчитываемая от его максимального значения. Фазу поля j, при которой частица пролетает через ускоряющий промежуток, называют для краткости фазой частицы.

  Чтобы частица двигалась синхронно с изменением ускоряющего поля, её частота обращения w должна быть равна или кратна частоте w₀ электрического поля: w₀= qw, где q — целое число (кратность резонанса). Тогда частица будет проходить ускоряющие электроды при одном и том же значении фазы j и при каждом прохождении получать от поля одну и ту же энергию. Поэтому она будет всё время ускоряться.

  Такая ситуация выполняется в циклотроне — единственном резонансном ускорителе, который существовал до открытия принципа А. В циклотроне частицы движутся в постоянном магнитном поле Н с постоянной частотой обращения w = eH/mc (где m — масса частицы, с — скорость света). Поэтому при частоте ускоряющего электрического поля w₀ = w для всех частиц наблюдается точный резонанс с полем.

  Однако при достижении достаточно большой энергии массу m уже нельзя считать постоянной: начинает сказываться эффект увеличения массы частицы с ростом энергии (см. Относительности теория). Возрастание массы приводит к уменьшению частоты обращения w и к нарушению резонанса между движением частицы и ускоряющим полем. Частицы перестают получать энергию от электрического поля и выпадают из режима ускорения. Поэтому в обычном циклотроне существует предельная энергия, выше которой ускорение невозможно. Для протонов этот предел энергии составляет примерно 20 Мэв.

  Для сохранения резонанса можно, например, медленно снижать частоту w₀ ускоряющего поля в соответствии с уменьшением w или медленно изменять напряжённость магнитного поля Н, чтобы компенсировать уменьшение частоты w (или вместе и то и другое).

  Но в ускорителе одновременно ускоряются сотни и тысячи миллиардов частиц, имеющих разброс по энергиям, а значит, и по массам. Следовательно, частицы будут иметь различные частоты обращения w. Поэтому невозможно осуществить точный резонанс с ускоряющим полем для движения всего множества ускоряемых частиц. До открытия принципа А. эта трудность казалась непреодолимой.

  Векслер и Макмиллан показали, что именно благодаря зависимости частоты обращения частиц от их энергии (массы), приводящей к нарушению точного синхронизма движения частиц с ускоряющим полем, само поле будет автоматически осуществлять для большого количества частиц подстройку синхронизма в среднем. Иными словами, в случае, когда w зависит от энергии, ускоряющее поле частоты w₀ (которая может и медленно меняться) заставляет частицы двигаться по орбитам с частотами, в среднем равными (или кратными) частоте w₀, т. е. реализует резонанс в среднем; при этом фазы частиц колеблются и концентрируются около одной фазы j₀ (см. ниже), которая называется синхронной, или равновесной. Это явление и называется А.

  Т. о., А. приводит к тому, что частицы в среднем обращаются синхронно с изменением ускоряющего поля: w_ср = w₀.

  Рассмотрим, как осуществляется А. в циклическом ускорителе с однородным и постоянным во времени магнитным полем и при q = 1. Частота обращения частиц в таком ускорителе обратно пропорциональна их массе, а следовательно, их полной энергии (равной сумме энергии покоя и кинетической энергии). Синхронная частица (воображаемая частица, которая движется в точном резонансе с ускоряющим полем) будет ускоряться при одной и той же фазе j₀ и каждый раз получать энергию eV₀ cos j₀. Для того чтобы движение частиц по орбитам было устойчивым, т. е. чтобы частицы с фазами j¹j₀ не выпадали из режима ускорения, синхронная фаза j₀ должна быть положительной — находиться на спаде ускоряющего напряжения (рис. 1). Действительно, частица с меньшей энергией, для которой частота обращения w > w₀ и которая в некоторый момент движется вместе с синхронной, в дальнейшем будет опережать синхронную, попадать в ускоряющий промежуток раньше и ускоряться при меньшей фазе j₁<j₀. Следовательно, она получит большую энергию: eV₀ cos j₁ > eV₀ cos j₀, и её частота начнёт уменьшаться, так что в какой-то момент наступит точный резонанс, w = w₀. Но этот резонанс является только мгновенным — ведь частица по-прежнему будет получать от поля большую энергию и её частота w будет некоторое время продолжать уменьшаться и станет меньше синхронной, w < w₀. Тогда частица начнёт отставать от синхронной, будет получать меньшую энергию от ускоряющего поля, чем синхронная частица, и её частота станет вновь расти.

  Аналогичный процесс происходит и с частицей, отставшей от синхронной и попадающей в ускоряющий промежуток несколько позже, при фазе j₂>j₀. Такая частица будет получать от поля меньшую энергию, её частота начнёт расти, и частица будет догонять синхронную.

  Т. о., частоты обращения частиц совершают медленные по сравнению с частотой обращения колебания около значения w₀. Соответственно колеблются фазы частиц около значения j₀, а средняя их фаза является устойчивой: j_ср = j₀ (отсюда название — фазовая устойчивость, или А.). Поэтому в среднем будет автоматически поддерживаться синхронизм между движением частиц и ускоряющим полем. Одновременно совершают колебания и другие характеристики движения частиц (энергия, радиус орбиты) около их равновесных значений, отвечающих синхронной частице. Эти колебания фазы и связанные с ними колебания радиуса орбиты частиц называются радиально-фазовыми.

  А. действует и в линейных резонансных ускорителях протонов, в которых (в отличие от циклических ускорителей) частота прохождения частицей последовательных ускоряющих промежутков (расположенных по прямой линии) прямо пропорциональна скорости её движения, т. е. увеличивается с ростом энергии. Однако устойчивая синхронная фаза в линейных ускорителях отрицательна — лежит на подъёме ускоряющего электрического напряжения (рис. 2). Тогда при пролёте частицей ускоряющего промежутка поле возрастает, так что отстающая частица (с фазой j₂>j₀) получает большую энергию и начинает догонять синхронную частицу, а опережающая (с фазой j₁<j₀) — меньшую энергию и также начинает приближаться к синхронной.

  Принцип А. оказал революционизирующее влияние на развитие ускорительной техники. Появилось семейство разнообразных ускорителей, работающих на основе А.: циклические ускорители электронов (синхротроны) на энергии до 7 Гэв и протонов (синхрофазотроны, фазотроны и др.) до энергии 75 Гэв, циклические ускорители с переменной кратностью q (микротроны), линейные резонансные ускорители протонов на энергии до 70 Мэв. А. отсутствует, когда частота обращения частиц не зависит от их энергии (изохронные циклотроны), а в линейных ускорителях — когда скорость движения частиц приближается к скорости света и практически перестаёт зависеть от энергии (линейные ускорители электронов на энергии выше 10 Мэв).

  Об А. в ускорителях со знакопеременной (сильной) фокусировкой см. Ускорители заряженных частиц.

  Лит. см. при статье Ускорители заряженных частиц.

  М. С. Рабинович.

Рис. 1. Синхронная фаза j₀ > 0.

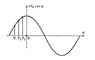
Рис. 2. Синхронная фаза j₀< 0.

Оглавление