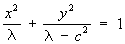 (*)
(*)Софокусные кривые, конфокальные кривые [от лат. con (cum) — с, вместе и фокус], линии второго порядка, имеющие общие фокусы. Если F и F'— две данные точки плоскости, то через каждую точку плоскости проходит один эллипс и одна гипербола, имеющие F и F' своими фокусами (рис. 1).
Каждый эллипс ортогонален любой софокусной с ним гиперболе, т. е. пересекается с ней (в четырёх точках) под прямым углом (углом между двумя кривыми в точке пересечения называется угол между их касательными). Всё множество софокусных эллипсов и гипербол в надлежащей системе координат определяется уравнением
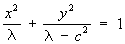 (*)
(*)
где с — расстояние фокусов от начала координат, а l — переменный параметр. При l > с2 это уравнение определяет эллипс, при 0< l< с2 — гиперболу (при l < 0 — мнимую линию 2-го порядка). Если один из фокусов стремится к бесконечности, то в пределе получаются два семейства софокусных парабол (рис. 2); любые две параболы, относящиеся к разным семействам, также ортогональны друг другу. При помощи софокусных эллипсов и гипербол на плоскости вводится система т. н. эллиптических координат. Именно, если М (х, у) — произвольная точка плоскости, то, подставляя ее координаты х и у в уравнение (*), получим квадратное уравнение для l; корни его l1, l2 называются эллиптическими координатами точки М. Сами софокусные эллипсы и гиперболы составляют координатную сеть эллиптической координатной системы, т. с. определяются уравнениями l = const. l2 = const.

Рис. 1 к ст. Софокусные кривые.

Рис. 2 к ст. Софокусные кривые.