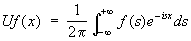
Унитарный оператор, обобщение понятия вращения евклидова пространства на бесконечномерный случай. Именно, У. о. – оператор вращений гильбертова пространства вокруг нулевой точки. Оператор U, отображающий гильбертово пространство Н на себя, называется У. о., если (f, g) = (Uf, Ug)(см. Скалярное произведение) для любых двух векторов f и g из Н. У. о. не изменяет длин векторов в Н и углов между ними и является линейным оператором. Он имеет обратный оператор U1, также являющийся У. о.; при этом U1 = U*, где U* – сопряжённый оператор. Примером У. о. может служить оператор Фурье – Планшереля, ставящий в соответствие каждой функции f (x), – ¥ < х < + ¥, с интегрируемым квадратом модуля функцию
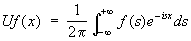
(см. Фурье преобразование). См. также Операторов теория, Спектральный анализ линейных операторов.