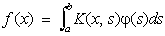Фредгольма уравнение, интегральные уравнения вида:

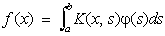,     (1)

a £ x, s £ b, (Ф. у. 1-го рода) и

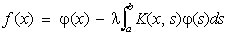,     (2)

a £ x, s £ b,

(Ф. у. 2-го рода), где К (х, s) — заданная непрерывная функция от x и s, называемая ядром уравнения, f (x) — заданная функция, j(х) — искомая функция, l — параметр (см. Интегральные уравнения). Уравнения (1) и (2) были изучены в 1900—1903 Э. Фредгольмом. Теория Ф. у. 2-го рода проще и они чаще используются в приложениях. Построение устойчивых решений Ф. у. 1-го рода в общем случае возможно лишь с помощью специальных регуляризирующих алгоритмов решения некорректно поставленных задач. Если l не является собственным значением уравнения (2), то это уравнение имеет единственное непрерывное решение, определяемое формулой:

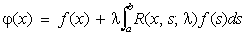,     (3)

где R (x, s; l) = D (x, s, l)/D (l) называется резольвентой уравнения (2). Здесь

,

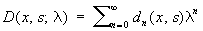d₀(x, s) = K (x, s),

,

,

, .

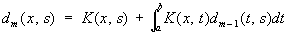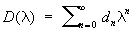  Лит.: см. при ст. Интегральные уравнения.

Оглавление