 ,
, 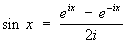 .
.Эйлера формулы в математике, важнейшие формулы, установленные Л. Эйлером.
1) Э. ф., связывающие тригонометрические функции с показательной (1743):
eix = cos х + i sin х,
 ,
, 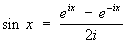 .
.
2) Э. ф., дающая разложение функции sin х в бесконечное произведение (1740):
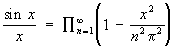 .
.
3) Тождество Эйлера о простых числах:
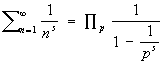 ,
,
где s = 1, 2,..., и произведение берётся по всем простым числам р.
4) Тождество Эйлера о четырёх квадратах:
(a2 +b2 + c2 + d2)(p2 + q2 + r2 + s2 = x2+y2+z2+t2, где
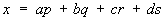 ,
,
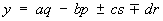 ,
,
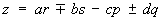 ,
,
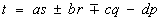 .
.
5) формула Эйлера о кривизнах (1760):
 .
.
Она даёт выражение кривизны 1/R любого нормального сечения поверхности через её главные кривизны 1/R1 и 1/R2 и угол j между одним из главных направлений и данным направлением.
Эйлеру принадлежит также Эйлера—Маклорена формула суммирования, Эйлера—Фурье формулы для коэффициентов разложений функций в тригонометрические ряды.
Лит. см. при ст. Эйлер.