Эллипс, линия пересечения круглого конуса с плоскостью, встречающей одну его полость (рис. 1). Э. может быть также определён как геометрическое место точек М плоскости, для которых сумма расстояний до двух определенных точек F₁ и F₂ (фокусов Э.) этой плоскости есть величина постоянная. Если выбрать систему координат xOy так, как указано на рис. 2 (OF₁ =OF₂ = с), то уравнение Э. примет вид:

   (*)

  (2a = F₁M + F₂M, ). Э. — линия второго порядка; она симметрична относительно осей AB и CD; точка О — центр Э. — является его центром симметрии; отрезки AB = 2a и CD = 2b называются соответственно большой и малой осями Э.; число е = с/а<1 — эксцентриситет Э. (при е = 0, то есть при а = b, Э. есть окружность). Прямые, уравнения которых x = —а/е и х = а/е, называются директрисами Э.; отношение расстояния точки Э. до ближайшего фокуса к расстоянию до ближайшей директрисы постоянно и равно эксцентриситету. Точки А, В, С, D пересечения Э. с осями Ox и Оу называются его вершинами. См. также Конические сечения.

Рис. 2. к ст. Эллипс.

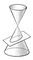
Рис. 1. к ст. Эллипс.

Оглавление