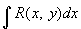Эллиптические интегралы, интегралы вида

,

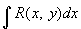где R (x, у) — рациональная функция х и 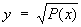, а Р (х) — многочлен 3-й или 4-й степени без кратных корней.

  Под Э. и. первого рода понимают интеграл

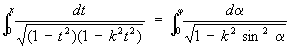 (1)

под Э. и. второго рода — интеграл

где k — модуль Э. и., 0 < k < 1 (х = sin j, t = sin a. Интегралы в левых частях равенств (1) и (2) называются Э. и. в нормальной форме Якоби, интегралы в правых частях — Э. и. в нормальной форме Лежандра. При х = 1 или j = p/2 Э. и называются полными и обозначаются, соответственно, через

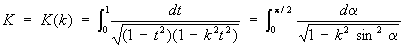
и

  Своё назв. Э. и. получили в связи с задачей вычисления длины дуги эллипса и = a sin a, v = b cos a(a < b). Длина дуги эллипса выражается формулой

где  — эксцентриситет эллипса. Длина дуги четверти эллипса равна E (k). Функции, обратные Э. и., называются эллиптическими функциями.

Оглавление