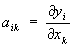Якобиан, функциональный определитель ½a_ik½₁ⁿ с элементами 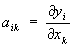, где y_i = f_i (X₁,..., X_n), l £ i £ n, — функции, имеющие непрерывные частные производные в некоторой области А; обозначение:

  .

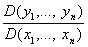  Введён К. Якоби (1833, 1841). Если, например, n = 2, то система функций

  y₁ = f₁ (. x₁, x₂), y₂ = f₂ (x₁, x₂) (1)

  задаёт отображение области D, лежащей на плоскости x₁, x₂, на часть плоскости y₁, y₂. Роль Я. для этого отображения во многом аналогична роли производной для функции одной переменной. Например, абсолютное значение Я. в некоторой точке М равно коэффициенту искажения площадей в этой точке (т. е. пределу отношения площади образа окрестности точки М к площади самой окрестности, когда размеры окрестности стремятся к нулю). Я. в точке М положителен, если отображение (1) не меняет ориентации в окрестности точки М, и отрицателен в противоположном случае. Если Я. не обращается в нуль в области D и j (y₁, у₂) — функция, заданная в области D₁ (образе D), то

(формула замены переменных в двойном интеграле). Аналогичная формула имеет место для кратных интегралов. Если Я. отображения (1) не обращается в нуль в области Д, то существует обратное отображение

  x₁ = j₁ (y₁, y₂), x₁ = j₂(y₁, y₂),

  причём

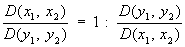
  (аналог формулы дифференцирования обратной функции). Это утверждение находит многочисленные применения в теории неявных функций. Для возможности явного выражения в окрестности точки М (x₁⁽⁰⁾,..., x_n ⁽⁰, y₁⁽⁰⁾,..., y_m ⁽⁰⁾) функций y₁,..., у_т, неявно заданных уравнениями F_k (x₁,..., x_n, y₁,..., у_м) = 0, (2)

  1 £ k £ m,

  достаточно, чтобы координаты точки М удовлетворяли уравнениям (2), функции Fk имели непрерывные частные производные и Я.

  был отличен от нуля в точке М.

  Лит.: Кудрявцев Л. Д., Математический анализ, 2 изд., т. 2, М., 1973; Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971.

Оглавление