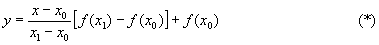
Интерполяция в математике и статистике, отыскание промежуточных значений величины по некоторым известным её значениям. Например, отыскание значений функции f (x) в точках х, лежащих между точками (узлами И.) x₀ < x₁ < ... < x_n, по известным значениям y_i = f (x_i) (где i = 0, 1, ..., n). В случае, если х лежит вне интервала, заключённого между x₀ и x_n, аналогичная задача наывается задачей экстраполяции. При простейшей линейной И. значение f (x) в точке х, удовлетворяющей неравенствам x₀ < x < x₁, принимают равным значению

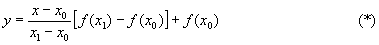
линейной функции, совпадающей с f (x) в точках х = x₀ и х = x₁. Задача И. со строго математической точки зрения является неопределённой: если про функцию f (x) ничего неизвестно, кроме её значений в точках x₀, x₁,..., х_n, то её значение в точке х, отличной от всех этих точек, остаётся совершенно произвольным. Задача И. приобретает определённый смысл, если функция f (x) и её производные подчинены некоторым неравенствам. Если, например, заданы значения f (x₀) и f (x₁) и известно, что при x₀ < x < x₁ выполняется неравенство |f¢’’(x)| £ M, то погрешность формулы (*) может быть оценена при помощи неравенства

  Более сложные интерполяционные формулы имеет смысл применять лишь в том случае, если есть уверенность в достаточной «гладкости» функции, т. е. в том, что она обладает достаточным числом не слишком быстро возрастающих производных.

  Кроме вычисления значений функций, И. имеет и многочисленные другие приложения (например, при приближённом интегрировании, приближённом решении уравнений, в статистике при сглаживании рядов распределения с целью устранения случайных искажений).

  Лит.: Гончаров В. Л., Теория интерполирования и приближения функций, 2 изд., М., 1954; Крылов А. Н., Лекции о приближённых вычислениях, 6 изд., М., 1954; Юл Дж. Э., Кендэл М. Дж., Теория статистики, пер. с англ., 14 изд., М., 1960.

Оглавление