Интерференция света, сложение световых волн, при котором обычно наблюдается характерное пространственное распределение интенсивности света (интерференционная картина) в виде чередующихся светлых и тёмных полос вследствие нарушения принципа сложения интенсивностей (см. Интерференция волн). Некоторые явления И. с. наблюдались ещё И. Ньютоном, но не могли быть объяснены с точки зрения его корпускулярной теории (см. Свет, Оптика). Правильное объяснение И. с. как типично волнового явления было дано в начале 19 в. Т. Юнгом и О. Френелем.
И. с. возникает только в случае, если разность фаз постоянна во времени, т. е. волны когерентны (см. Когерентность). До создания лазеров когерентные световые пучки могли быть получены только путём разделения и последующего сведения лучей, исходящих из одного и того же источника света. При этом разность фаз этих колебаний постоянна и определяется только разностью путей, проходимых лучами, или разностью хода D. Существует несколько способов создания когерентных пучков света. Например, в опыте Френеля (рис. 1) два плоских зеркала I и II, образующих двугранный угол, близкий к 180°, дают два мнимых изображения S1 и S2 источника S. На экране AB получается светлая полоса при разности хода D лучей S1M и S2M, равной чётному числу полуволн, и тёмная полоса — при D, равной нечётному числу полуволн. Другой способ был предложен Юнгом (рис. 2). Свет из отверстия S падает на экран AB с двумя отверстиями (или щелями) S1 и S2. И. с. наблюдается на экране CD. Расстояние между соседними светлыми или тёмными интерференционными полосами Dх » l/a, где a — угол S1MS2, под которым сходятся интерферирующие лучи. В этих опытах И. с. наблюдается только при сложении волн, испущенных из одной и той же точки источника. Интерференционные полосы, соответствующие разным точкам источника, сдвинуты относительно друг друга, и при наложении интерференционные картины смазываются. Предельный размер источника, ещё дающего чёткую интерференционную картину, определяется соотношением d = l/b, где b — угол, под которым расходятся лучи из источника (например, ÐS1SS2 на рис. 2).
Это ограничение не имеет места в случае И. с., отражённого от двух поверхностей плоской или слабоклиновидной прозрачной пластинки (рис. 3). При этом между отражёнными лучами возникает разность хода D = 2hn cos i’¢ + l/2, где h — толщина пластинки, n — её показатель преломления, i¢ — угол преломления. Добавочная разность хода l/2 возникает из-за различия сдвига фазы при отражении от верхней и нижней поверхностей пластинки. В строго плоскопараллельных пластинках (с точностью до долей l) одинаковую разность хода будут иметь лучи, падающие на пластинку под одним и тем же углом i, а интерференционные полосы в этом случае называются полосами равного наклона. Они локализованы в бесконечности, поэтому их можно наблюдать в главной фокальной плоскости линзы. В тонких пластинках переменной толщины линии максимумов и минимумов проходят по точкам, соответствующим равной толщине пластинки, и называются полосами равной толщины. Они локализованы в плоскости пластинки. При этом данная интерференционная полоса в монохроматическом свете вычерчивает линию, соответствующую одной и той же толщине пластинки (рис. 4). Если свет не монохроматический, происходит наложение описанных картин для различных длин волн (между собой не интерферирующих); причём положения максимумов и минимумов смещены, поэтому в случае тонкой пластинки наблюдатель видит последовательность цветных полос. Этим явлением И. с. в тонких плёнках объясняются радужная окраска пятен масла или нефти на воде, цвета побежалости на закалённых металлах и др. И. с. в тонких плёнках играет большую роль при просветлении оптики, в интерференциальных светофильтрах, в интерференциальной микроскопии и др. И. с. в тонких плёнках изучается в оптике тонких слоев.
Возможность наблюдения И. с. зависит от степени монохроматичности света. В белом свете можно наблюдать только несколько интерференционных полос вблизи D = 0, которые в этом случае окрашены, потому что положение максимумов и минимумов зависит от длины волны. Если из источника света выделена одна узкая спектральная линия, максимальная разность хода Dmax может достигать нескольких десятков см. Чёткие интерференционные полосы ещё можно наблюдать при Dmax » l2/Dl, где Dl — ширина спектра. Dmax можно связать со временем t, в течение которого фаза волны не сбивается, т. е. излучается волна в виде отрезка синусоиды («цуг волн»). При этом Dmax оказывается равной длине цуга: Dmax = l2/Dl = ct (c — скорость света), что поясняет невозможность И. с. при D > Dmax, так как соответствующие цуги в двух интерферирующих пучках перестают перекрываться друг другом.
Ограничения размеров источника в приведённых выше опытах снимаются, если источником света служит излучение лазера, которое обладает пространственной когерентностью, и И. с. может наблюдаться при сложении волн, испускаемых разными точками источника. Высокая монохроматичность лазерного излучения позволяет наблюдать И. с. при огромной разности хода.
При очень малых интенсивностях света, когда при помощи чувствительных приёмников регистрируются отдельные фотоны, И. с. проявляется как статистическое явление. Среднее число квантов, попавших на тот или другой участок экрана в течение определённого времени, даёт такое же распределение интенсивности, что и при обычном способе наблюдения. Это находится в полном соответствии с квантовой теорией, согласно которой И. с. происходит не в результате сложения разных фотонов, а в результате «интерференции фотона самого с собой».
И. с. имеет самое широкое применение для измерения длины волны излучения, исследования тонкой структуры спектральной линии, определения плотности, показателей преломления и дисперсионных свойств веществ, для измерения углов, линейных размеров деталей в длинах световой волны, для контроля качества оптических систем и многого другого. На использовании И. с. основано действие интерферометров и интерференционных спектроскопов; метод голографии также основан на И. с.
Важный случай И. с. — интерференция поляризованных лучей (см. Поляризация света). В общем случае, когда складываются две различно поляризованные когерентные световые волны, происходит векторное сложение их амплитуд, что приводит к эллиптической поляризации. Это явление наблюдается, например, при прохождении линейно поляризованного света через анизотропные среды. Попадая в такую среду, линейно поляризованный луч разделяется на 2 когерентных, поляризованных во взаимно перпендикулярных плоскостях луча. Вследствие различного состояния поляризации скорость их распространения в этой среде различна и между ними возникает разность фаз D, зависящая от расстояния, пройденного в веществе. Величина D будет определять состояние эллиптической поляризации; в частности, при D, равной целому числу полуволн, поляризация будет линейной.
Интерференцию поляризованных лучей широко используют в кристаллооптике для определения структуры и ориентации осей кристалла, в минералогии для определения минералов и горных пород, для обнаружения и исследования напряжений и деформаций в твёрдых телах, для создания особо узкополосных светофильтров и др.
Лит.: Ландсберг Г. С., Оптика. 4 изд., М., 1957 (Общий курс физики, т. 3); Вавилов С. И., Микроструктура света, ч. 2, М., 1950; Борн М., Вольф Э., Основы оптики, пер. с англ., М., 1970.
М. Д. Галанин.
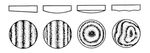
Рис. 4. Типичные случаи полос равной толщины.

Рис. 3. Интерференция в плоскопараллельной пластинке.

Рис. 1. Схема опыта Френеля.
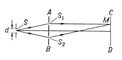
Рис. 2. Схема опыта Юнга.