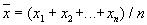
Больших чисел закон, общий принцип, в силу которого совокупное действие большого числа случайных факторов приводит, при некоторых весьма общих условиях, к результату, почти не зависящему от случая. Точная формулировка и условия применимости Б. ч. з. даются в теории вероятностей. Б. ч. з. является одним из выражений диалектической связи между случайностью и необходимостью. Первая точно доказанная теорема принадлежит Я. Бернулли (опубликована после его смерти, в 1713, см. Бернулли теорема). Теорема Бернулли была обобщена С. Пуассоном, в сочинении которого «Исследование о вероятности суждения» (1837) впервые появился термин «закон больших чисел». Значительно более общее понимание этого термина основано на работе П. Л. Чебышева «О средних величинах» (1867). В этом современном понимании Б. ч. з. утверждает, что при некоторых подлежащих точному указанию условиях среднее арифметическое
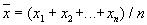
достаточно большого числа n случайных величин Xk с вероятностью, сколь угодно близкой к единице, сколь угодно мало отличается от своего математического ожидания
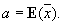
Новым и весьма плодотворным оказался предложенный Чебышевым метод доказательства Б. ч. з., основанный на применении т. н. Чебышева неравенства.
Для независимых случайных величин, имеющих одинаковые распределения вероятностей и конечное математическое ожидание а, Б. ч. з. утверждает, что при любом e > 0 вероятность неравенства |х - а| < e стремится к единице при n ®¥. Порядок отклонений  от а указывается предельными теоремами теории вероятностей. В типичных случаях отклонения имеют порядок
от а указывается предельными теоремами теории вероятностей. В типичных случаях отклонения имеют порядок

Соответственно, случайные отклонения суммы
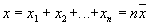
от её математического ожидания na растут как

Этот факт (называемый в упрощённых популярных изложениях «законом корня квадратного из n») даёт некоторое, хотя и грубое, представление о характере действия Б. ч. з.
Наглядное объяснение смысла и значения Б. ч. з. даёт следующий пример. Пусть в замкнутом сосуде заключено N молекул газа. В соответствии с кинетической теорией каждая молекула беспорядочно движется внутри сосуда, испытывая множество столкновений с другими молекулами и стенками сосуда. Ударяясь о какую-либо площадку s стенки в течение выбранного промежутка времени в t секунд, отдельная молекула сообщает этой площадке импульс fk (см. Ударный импульс). Импульс fk является типичной случайной величиной, т.к. состояние рассматриваемого газа определяет лишь математическое ожидание а = E (fk) этого импульса, фактическое же значение импульса данной молекулы за данный промежуток времени может быть самым различным (начиная от нуля — в случае, если за данный промежуток времени данная молекула не ударялась о площадку s). Сумма

импульсов всех молекул, сообщаемых площадке s за данный промежуток времени, является также случайной величиной с математическим ожиданием, равным А = Na. Однако в силу Б. ч. з. (который проявляется здесь с исключительной точностью благодаря тому, что число N очень велико) F в действительности оказывается почти независимым от случайных обстоятельств движения отдельных молекул, а именно — почти точно равным своему математическому ожиданию А. Этим, с точки зрения кинетической теории, и объясняется тот факт, что давление газа на площадку s является практически строго постоянным, а не колеблется беспорядочно.
Часто приходится применять Б. ч. з. и в такой обстановке, когда количество случайных слагаемых не столь велико, как в примере с газовыми молекулами; тогда отклонения суммы случайных величин от её математического ожидания могут быть значительными. В этом случае крайне важно уметь оценивать размеры этих отклонений. Пусть, например, из 1000 партий каких-либо изделий, по 100 шт. в каждой, взято для испытания наудачу по 10 шт. из каждой партии и среди испытанных 10 000 шт. обнаружено 125 дефектных. Если обозначить nк число дефектных изделий в k-й партии, то общее число дефектных изделий равно

математическое ожидание числа дефектных изделий среди тех десяти, которые взяты для испытаний из k-й партии, равно Sk = (10/100) nk, а математическое ожидание общего числа дефектных изделий в 1000 пробах по 10 штук равно
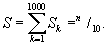
В силу Б. ч. з. естественно считать, что n/10 ~ 125, т. е. среди 100 000 изделий во всех партиях имеется приблизительно 1250 дефектных. Более точное исследование с помощью теории вероятностей приводит к такому результату: если выборка изделий из каждой партии была действительно случайной, то можно с достаточной уверенностью утверждать, что фактически 1000 < n < 1500, но уже оценка 1100 < n < 1400 не была бы достаточно надёжной, а для оценки 1200 < n < 1300 совсем не имеется серьёзных оснований. Получить более точную оценку для n можно, лишь испытав большее число изделий.
Условие независимости слагаемых в большинстве применений Б. ч. з. если и выполняется, то лишь с тем или иным приближением. Так, уже в первом примере движения отдельных молекул газа нельзя, строго говоря, считать независимыми. Поэтому важно исследование условий применимости Б. ч. з. к случаю зависимых слагаемых. Основные математические работы в этом направлении принадлежат А. А. Маркову, С. Н. Бернштейну и А. Я. Хинчину. Качественно результаты их исследований сводятся к тому, что Б. ч. з. применим, если между слагаемыми с далёкими номерами зависимость достаточно слаба. Таково, например, положение в рядах метеорологических наблюдений над температурой или давлением воздуха.
Математическая сторона вопросов, связанных с Б. ч. з., освещена также в ст. Предельные теоремы теории вероятностей и Вероятностей теория. В применениях Б. ч. з. необходимо тщательно проверять соответствие условий его применимости реальной обстановке.
Лит.: Bernoulli J., Ars conjectandi, opus posthumum, Basileae, 1713 (в рус. пер.— Часть 4 соч. Я. Бернулли..., СПБ, 1913); Poisson S.-D., Recherches sur la probabilité des jugements en matière criminelle et en matière civile, précédées des règles générales du calcul des probabilités, P., 1837; Чебышев П. Л., О средних величинах, Полн. собр. соч., т. 2, М.—Л., 1947, с. 431—37; Гнеденко Б. В., Курс теории вероятностей, 4 изд., М., 1965.
Л. Н. Колмогоров.