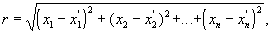
Геометрия (греч. geometria, от ge — Земля и metreo — мерю), раздел математики, изучающий пространственные отношения и формы, а также другие отношений и формы, сходные с пространственными по своей структуре.
Происхождение термина «Г.", что буквально означает «землемерие», можно объяснить следующими словами, приписываемыми древнегреческому учёному Евдему Родосскому (4 в. до н. э.): «Геометрия была открыта египтянами и возникла при измерении Земли. Это измерение было им необходимо вследствие разлития р. Нил, постоянно смывавшего границы». Уже у древних греков Г. означала математическую науку, в то время как для науки об измерении Земли был введён термин геодезия. Судя по сохранившимся отрывкам древнеегипетских сочинений, Г. развилась не только из измерений Земли, но также из измерений объёмов и поверхностей при земляных и строительных работах и т.п.
Первоначальные понятия Г. возникли в результате отвлечения от всяких свойств и отношений тел, кроме взаимного расположения и величины. Первые выражаются в прикосновении или прилегании тел друг к другу, в том, что одно тело есть часть другого, в расположении «между», «внутри» и т.п. Вторые выражаются в понятиях «больше», «меньше», в понятии о равенстве тел.
Путём такого же отвлечения возникает понятие геометрического тела. Геометрическое тело есть абстракция, в которой сохраняются лишь форма и размеры в полном отвлечении от всех других свойств. При этом Г., как свойственно математике вообще, совершенно отвлекается от неопределённости и подвижности реальных форм и размеров и считает все исследуемые ею отношения и формы абсолютно точными и определёнными. Отвлечение от протяжения тел приводит к понятиям поверхности, линии и точки. Это явно выражено, например, в определениях, данных Евклидом: «линия есть длина без ширины», «поверхность есть то, что имеет длину и ширину». Точка без всякого протяжения есть абстракция, отражающая возможность неограниченного уменьшения всех размеров тела, воображаемый предел его бесконечного деления. Дальше возникает общее понятие о геометрической фигуре, под которой понимают не только тело, поверхность, линию или точку, но и любую их совокупность.
Г. в первоначальном значении есть наука о фигурах, взаимном расположении и размерах их частей, а также о преобразованиях фигур. Это определение вполне согласуется с определением Г. как науки о пространственных формах и отношениях. Действительно, фигура, как она рассматривается в Г., и есть пространственная форма; поэтому в Г. говорят, например, «шар», а не «тело шарообразной формы»; расположение и размеры определяются пространственными отношениями; наконец, преобразование, как его понимают в Г., также есть некоторое отношение между двумя фигурами — данной и той, в которую она преобразуется.
В современном, более общем смысле, Г. объемлет разнообразные математические теории, принадлежность которых к Г. определяется не только сходством (хотя порой и весьма отдалённым) их предмета с обычными пространственными формами и отношениями, но также тем, что они исторически сложились и складываются на основе Г. в первоначальном её значении и в своих построениях исходят из анализа, обобщения и видоизменения её понятий. Г. в этом общем смысле тесно переплетается с другими разделами математики и её границы не являются точными. См. разделы Обобщение предмета геометрии и Современная геометрия.
Развитие геометрии. В развитии Г. можно указать четыре основных периода, переходы между которыми обозначали качественное изменение Г.
Первый — период зарождения Г. как математической науки — протекал в Древнем Египте, Вавилоне и Греции примерно до 5 в. до н. э. Первичные геометрические сведения появляются на самых ранних ступенях развития общества. Зачатками науки следует считать установление первых общих закономерностей, в данном случае — зависимостей между геометрическими величинами. Этот момент не может быть датирован. Самое раннее сочинение, содержащее зачатки Г., дошло до нас из Древнего Египта и относится примерно к 17 в. до н. э., но и оно, несомненно, не первое. Геометрические сведения того периода были немногочисленны и сводились прежде всего к вычислению некоторых площадей и объёмов. Они излагались в виде правил, по-видимому, в большой мере эмпирического происхождения, логические же доказательства были, вероятно, ещё очень примитивными. Г., по свидетельству греческих историков, была перенесена в Грецию из Египта в 7 в. до н. э. Здесь на протяжении нескольких поколений она складывалась в стройную систему. Процесс этот происходил путём накопления новых геометрических знаний, выяснения связей между разными геометрическими фактами, выработки приёмов доказательств и, наконец, формирования понятий о фигуре, о геометрическом предложении и о доказательстве.
Этот процесс привёл, наконец, к качественному скачку. Г. превратилась в самостоятельную математическую науку: появились систематические её изложения, где её предложения последовательно доказывались. С этого времени начинается второй период развития Г. Известны упоминания систематические изложения Г., среди которых данное в 5 в. до н. э. Гиппократом Хиосским. Сохранились же и сыграли в дальнейшем решающую роль появившиеся около 300 до н. э. «Начала» Евклида. Здесь Г. представлена так, как её в основном понимают и теперь, если ограничиваться элементарной геометрией; это наука о простейших пространственных формах и отношениях, развиваемая в логической последовательности, исходя из явно формулированных основных положений — аксиом и основных пространственных представлений. Г., развиваемую на тех же основаниях (аксиомах), даже уточнённую и обогащенную как в предмете, так и в методах исследования, называется евклидовой геометрией. Ещё в Греции к ней добавляются новые результаты, возникают новые методы определения площадей и объёмов (Архимед, 3 в. до н. э.), учение о конических сечениях (Аполлоний Пергский, 3 в. до н. э.), присоединяются начатки тригонометрии (Гиппарх, 2 в. до н. э.) и Г. на сфере (Менелай, 1 в. н. э.). Упадок античного общества привёл к сравнительному застою в развитии Г., однако она продолжала развиваться в Индии, в Средней Азии, в странах арабского Востока.
Возрождение наук и искусств в Европе повлекло дальнейший расцвет Г. Принципиально новый шаг был сделан в 1-й половине 17 в. Р. Декартом, который ввёл в Г. метод координат. Метод координат позволил связать Г. с развивавшейся тогда алгеброй и зарождающимся анализом. Применение методов этих наук в Г. породило аналитическую Г., а потом и дифференциальную. Г. перешла на качественно новую ступень по сравнению с Г. древних: в ней рассматриваются уже гораздо более общие фигуры и используются существенно новые методы. С этого времени начинается третий период развития Г. Аналитическая геометрия изучает фигуры и преобразования, задаваемые алгебраическими уравнениями в прямоугольных координатах, используя при этом методы алгебры. Дифференциальная геометрия, возникшая в 18 в. в результате работ Л. Эйлера, Г. Монжа и др., исследует уже любые достаточно гладкие кривые линии и поверхности, их семейства (т. е. их непрерывные совокупности) и преобразования (понятию «дифференциальная Г.» придаётся теперь часто более общий смысл, о чём см. в разделе Современная геометрия). Её название связано в основном с её методом, исходящим из дифференциального исчисления. К 1-й половине 17 в. относится зарождение проективной геометрии в работах Ж. Дезарга и Б. Паскаля. Она возникла из задач изображения тел на плоскости; её первый предмет составляют те свойства плоских фигур, которые сохраняются при проектировании с одной плоскости на другую из любой точки. Окончательное оформление и систематическое изложение этих новых направлений Г. были даны в 18 — начале 19 вв. Эйлером для аналитической Г. (1748), Монжем для дифференциальной Г. (1795), Ж. Понселе для проективной Г. (1822), причём само учение о геометрическом изображении (в прямой связи с задачами черчения) было ещё раньше (1799) развито и приведено в систему Монжем в виде начертательной геометрии. Во всех этих новых дисциплинах основы (аксиомы, исходные понятия) Г. оставались неизменными, круг же изучаемых фигур и их свойств, а также применяемых методов расширялся.
Четвёртый период в развитии Г. открывается построением Н. И. Лобачевским в 1826 новой, неевклидовой Г., называемой теперь Лобачевского геометрией. Независимо от Лобачевского в 1832 ту же Г. построил Я. Больяй (те же идеи развивал К. Гаусс, но он не опубликовал их). Источник, сущность и значение идей Лобачевского сводятся к следующему. В геометрии Евклида имеется аксиома о параллельных, утверждающая: «через точку, не лежащую на данной прямой, можно провести не более чем одну прямую, параллельную данной». Многие геометры пытались доказать эту аксиому, исходя из других основных посылок геометрии Евклида, но безуспешно. Лобачевский пришёл к мысли, что такое доказательство невозможно. Утверждение, противоположное аксиоме Евклида, гласит: «через точку, не лежащую на данной прямой, можно провести не одну, а по крайней мере две параллельные ей прямые». Это и есть аксиома Лобачевского. По мысли Лобачевского, присоединение этого положения к другим основным положениям Г. приводит к логически безупречным выводам. Система этих выводов и образует новую, неевклидову Г. Заслуга Лобачевского состоит в том, что он не только высказал эту идею, но действительно построил и всесторонне развил новую Г., логически столь же совершенную и богатую выводами, как евклидова, несмотря на её несоответствие обычным наглядным представлениям. Лобачевский рассматривал свою Г. как возможную теорию пространственных отношений; однако она оставалась гипотетической, пока не был выяснен (в 1868) её реальный смысл и тем самым было дано её полное обоснование (см. раздел Истолкования геометрии).
Переворот в Г., произведённый Лобачевским, по своему значению не уступает ни одному из переворотов в естествознании, и недаром Лобачевский был назван «Коперником геометрии». В его идеях были намечены три принципа, определившие новое развитие Г. Первый принцип заключается в том, что логически мыслима не одна евклидова Г., но и другие «геометрии». Второй принцип — это принцип самого построения новых геометрических теорий путём видоизменения и обобщения основных положений евклидовой Г. Третий принцип состоит в том, что истинность геометрической теории, в смысле соответствия реальным свойствам пространства, может быть проверена лишь физическим исследованием и не исключено, что такие исследования установят, в этом смысле, неточность евклидовой Г. Современная физика подтвердила это. Однако от этого не теряется математическая точность евклидовой Г., т.к. она определяется логической состоятельностью (непротиворечивостью) этой Г. Точно так же в отношении любой геометрической теории нужно различать их физическую и математическую истинность; первая состоит в проверяемом опытом соответствии действительности, вторая — в логической непротиворечивости. Лобачевский дал, т. о., материалистическую установку философии математики. Перечисленные общие принципы сыграли важную роль не только в Г., но и в математике вообще, в развитии её аксиоматического метода, в понимании её отношения к действительности.
Главная особенность нового периода в истории Г., начатого Лобачевским, состоит в развитии новых геометрических теорий — новых «геометрий» и в соответствующем обобщении предмета Г.; возникает понятие о разного рода «пространствах» (термин «пространство» имеет в науке два смысла: с одной стороны, это обычное реальное пространство, с другой — абстрактное «математическое пространство»). При этом одни теории складывались внутри евклидовой Г. в виде её особых глав и лишь потом получали самостоятельное значение. Так складывались проективная, аффинная, конформная Г. и др., предметом которых служат свойства фигур, сохраняющиеся при соответствующих (проективных, аффинных, конформных и др.) преобразованиях. Возникло понятие проективного, аффинного и конформного пространств; сама евклидова Г. стала рассматриваться в известном смысле как глава проективной Г. Др. теории, подобно геометрии Лобачевского, с самого начала строились на основе изменения и обобщения понятий евклидовой Г. Так, создавалась, например, многомерная Г.; первые относящиеся к ней работы (Г. Грасман и А. Кэли, 1844) представляли формальное обобщение обычной аналитической Г. с трёх координат на n. Некоторый итог развития всех этих новых «геометрий» подвёл в 1872 Ф. Клейн, указав общий принцип их построения.
Принципиальный шаг был сделан Б. Риманом (лекция 1854, опубликована 1867). Во-первых, он ясно формулировал обобщённое понятие пространства как непрерывной совокупности любых однородных объектов или явлений (см. раздел Обобщение предмета геометрии). Во-вторых, он ввёл понятие пространства с любым законом измерения расстояний бесконечно малыми шагами (подобно измерению длины линии очень малым масштабом). Отсюда развилась обширная область Г., т. н. риманова геометрия и её обобщения, нашедшая важные приложения в теории относительности, в механике и др.
В тот же период зародилась топология как учение о тех свойствах фигур, которые зависят лишь от взаимного прикосновения их частей и которые тем самым сохраняются при любых преобразованиях, не нарушающих и не вводящих новых прикосновений, т. е. происходящих без разрывов и склеиваний. В 20 в. топология развилась в самостоятельную дисциплину.
Так Г. превратилась в разветвленную и быстро развивающуюся в разных направлениях совокупность математических теорий, изучающих разные пространства (евклидово, Лобачевского, проективное, римановы и т.д.) и фигуры в этих пространствах.
Одновременно с развитием новых геометрических теорий велась разработка уже сложившихся областей евклидовой Г. — элементарной, аналитической и дифференциальной Г. Вместе с тем в евклидовой Г. появились новые направления. Предмет Г. расширился и в том смысле, что расширился круг исследуемых фигур, круг изучаемых их свойств, расширилось само понятие о фигуре. На стыке анализа и Г. возникла в 70-х гг. 19 в. общая теория точечных множеств, которая, однако, уже не причисляется к Г., а составляет особую дисциплину (см. Множеств теория). Фигура стала определяться в Г. как множество точек. Развитие Г. было тесно связано с глубоким анализом тех свойств пространства, которые лежат в основе евклидовой Г. Иными словами, оно было связано с уточнением оснований самой евклидовой Г. Эта работа привела в конце 19 в. (Д. Гильберт и др.) к точной формулировке аксиом евклидовой Г., а также других «геометрий».
Обобщение предмета геометрии. Возможность обобщения и видоизменения геометрических понятий легче всего уяснить на примере. Так, на поверхности шара можно соединять точки кратчайшими линиями — дугами больших кругов, можно измерять углы и площади, строить раз личные фигуры. Их изучение составляет предмет Г. на сфере, подобно тому, как планиметрия есть Г. на плоскости; Г. на земной поверхности близка к Г. на сфере. Законы Г. на сфере отличны от законов планиметрии; так, например, длина окружности здесь не пропорциональна радиусу, а растет медленнее и достигает максимума для экватора; сумма углов треугольника на сфере непостоянна и всегда больше двух прямых. Аналогично можно на любой поверхности проводить линии, измерять их длины, углы между ними, определять ограниченные ими площади. Развиваемая так Г. на поверхности называется её внутренней Г. (К. Гаусс, 1827). На неравномерно изогнутой поверхности соотношения длин и углов будут различными в разных местах, следовательно, она будет геометрически неоднородной, в отличие от плоскости и сферы. Возможность получения разных геометрических соотношений наводит на мысль, что свойства реального пространства могут лишь приближённо описываться обычной Г. Эта идея, впервые высказанная Лобачевским, нашла подтверждение в общей теории относительности.
Более широкая возможность обобщения понятий Г. выясняется из следующего рассуждения. Обычное реальное пространство понимают в Г. как непрерывную совокупность точек, т. е. всех возможных предельно точно определённых местоположений предельно малого тела. Аналогично непрерывную совокупность возможных состояний какой-либо материальной системы, непрерывную совокупность каких-либо однородных явлений можно трактовать как своего рода «пространство». Вот один из примеров. Опыт показывает, что нормальное человеческое зрение трёхцветно, т. е. всякое цветовое ощущение Ц есть комбинация — сумма трёх основных ощущений: красного К, зелёного З и синего С, с определёнными интенсивностями. Обозначая эти интенсивности в некоторых единицах через х, у, z, можно написать Ц = xK + уЗ + zC. Подобно тому, как точку можно двигать в пространстве вверх и вниз, вправо и влево, вперёд и назад, так и ощущение цвета Ц может непрерывно меняться в трёх направлениях с изменением составляющих его частей — красного, зелёного и синего. По аналогии можно сказать, что совокупность всех цветов есть трёхмерное пространство — «пространство цветов». Непрерывное изменение цвета можно изображать как линию в этом пространстве. Далее, если даны два цвета, например красный К и белый Б, то, смешивая их в разных пропорциях, получают непрерывную последовательность цветов, которую можно назвать прямолинейным отрезком КБ. Представление о том, что розовый цвет Р лежит между красным и белым и что более густой розовый лежит ближе к красному, не требует разъяснения. Т. о., возникают понятия о простейших «пространственных» формах (линия, отрезок) и отношениях (между, ближе) в пространстве цветов. Далее, можно ввести точное определение расстояния (например, по числу порогов различения, которое можно проложить между двумя цветами), определить поверхности и области цветов, подобно обычным поверхностям и геометрическим телам, и т.д. Так возникает учение о пространстве цветов, которое путём обобщения геометрических понятий отражает реальные свойства цветного зрения человека (см. Колориметрия).
Другой пример. Состояние газа, находящегося в цилиндре под поршнем, определяется давлением и температурой. Совокупность всех возможных состояний газа можно представлять поэтому как двумерное пространство. «Точками» этого «пространства» служат состояния газа; «точки» различаются двумя «координатами» — давлением и температурой, подобно тому как точки на плоскости различаются значениями их координат. Непрерывное изменение состояния изображается линией в этом пространстве.
Далее, можно представить себе любую материальную систему — механическую или физико-химическую. Совокупность всех возможных состояний этой системы называют «фазовым пространством». «Точками» этого пространства являются сами состояния. Если состояние системы определяется n величинами, то говорят, что система имеет n степеней свободы. Эти величины играют роль координат точки-состояния, как в примере с газом роль координат играли давление и температура. В соответствии с этим такое фазовое пространство системы называют n-мерным. Изменение состояния изображается линией в этом пространстве; отдельных области состояний, выделяемые по тем или иным признакам, будут областями фазового пространства, а границы областей будут поверхностями в этом пространстве. Если система имеет только две степени свободы, то её состояния можно изображать точками на плоскости. Так, состояние газа с давлением р и температурой Т изобразится точкой с координатами р и Т, а процессы, происходящие с газом, изобразятся линиями на плоскости. Этот метод графического изображения общеизвестен и постоянно используется в физике и технике для наглядного представления процессов и их закономерностей. Но если число степеней свободы больше 3, то простое графическое изображение (даже в пространстве) становится невозможным. Тогда, чтобы сохранить полезные геометрические аналогии, прибегают к представлению об абстрактном фазовом пространстве. Так, наглядные графические методы перерастают в это абстрактное представление. Метод фазовых пространств широко применяется в механике, теоретической физике и физической химии. В механике движение механической системы изображают движением точки в её фазовом пространстве. В физической химии особенно важно рассматривать форму и взаимное прилегание тех областей фазового пространства системы из нескольких веществ, которые соответствуют качественно различным состояниям. Поверхности, разделяющие эти области, суть поверхности переходов от одного качества к другому (плавление, кристаллизация и т.п.). В самой Г. также рассматривают абстрактные пространства, «точками» которых служат фигуры; так определяют «пространства» кругов, сфер, прямых и т.п. В механике и теории относительности вводят также абстрактное четырёхмерное пространство, присоединяя к трём пространственным координатам время в качестве четвёртой координаты. Это означает, что события нужно различать не только по положению в пространстве, но и во времени.
Т. о., становится понятным, как непрерывные совокупности тех или иных объектов, явлений, состояний могут подводиться под обобщённое понятие пространства. В таком пространстве можно проводить «линии», изображающие непрерывные последовательности явлений (состояний), проводить «поверхности» и определять подходящим образом «расстояния» между «точками», давая тем самым количественное выражение физическая понятия о степени различия соответствующих явлений (состояний), и т.п. Так по аналогии с обычной Г. возникает «геометрия» абстрактного пространства; последнее может даже мало походить на обычное пространство, будучи, например, неоднородным по своим геометрическим свойствам и конечным, подобно неравномерно искривленной замкнутой поверхности.
Предметом Г. в обобщённом смысле оказываются не только пространственные формы и отношения, но любые формы и отношения, которые, будучи взяты в отвлечении от своего содержания, оказываются сходными с обычными пространственными формами и отношениями. Эти пространственно-подобные формы действительности называют «пространствами» и «фигурами». Пространство в этом смысле есть непрерывная совокупность однородных объектов, явлений, состояний, которые играют роль точек пространства, причём в этой совокупности имеются отношения, сходные с обычными пространственными отношениями, как, например, расстояние между точками, равенство фигур и т.п. (фигура — вообще часть пространства). Г. рассматривает эти формы действительности в отвлечении от конкретного содержания, изучение же конкретных форм и отношений в связи с их качественно своеобразным содержанием составляет предмет других наук, а Г. служит для них методом. Примером может служить любое приложение абстрактной Г., хотя бы указанное выше применение n-мерного пространства в физической химии. Для Г. характерен такой подход к объекту, который состоит в обобщении и перенесении на новые объекты обычных геометрических понятий и наглядных представлений. Именно это и делается в приведённых выше примерах пространства цветов и др. Этот геометрический подход вовсе не является чистой условностью, а соответствует самой природе явлений. Но часто одни и те же реальные факты можно изображать аналитически или геометрически, как одну и ту же зависимость можно задавать уравнением или линией на графике.
Не следует, однако, представлять развитие Г. так, что она лишь регистрирует и описывает на геометрическом языке уже встретившиеся на практике формы и отношения, подобные пространственным. В действительности Г. определяет широкие классы новых пространств и фигур в них, исходя из анализа и обобщения данных наглядной Г. и уже сложившихся геометрических теорий. При абстрактном определении эти пространства и фигуры выступают как возможные формы действительности. Они, стало быть, не являются чисто умозрительными конструкциями, а должны служить, в конечном счёте, средством исследования и описания реальных фактов. Лобачевский, создавая свою Г., считал её возможной теорией пространственных отношений. И так же как его Г. получила обоснование в смысле её логической состоятельности и применимости к явлениям природы, так и всякая абстрактная геометрическая теория проходит такую же двойную проверку. Для проверки логической состоятельности существенное значение имеет метод построения математических моделей новых пространств. Однако окончательно укореняются в науке только те абстрактные понятия, которые оправданы и построением искусственной модели, и применениями, если не прямо в естествознании и технике, то хотя бы в др. математических теориях, через которые эти понятия так или иначе связываются с действительностью. Лёгкость, с которой математики и физики оперируют теперь разными «пространствами», достигнута в результате долгого развития Г. в тесной связи с развитием математики в целом и других точных наук. Именно вследствие этого развития сложилась и приобрела большое значение вторая сторона Г., указанная в общем определении, данном в начале статьи: включение в Г. исследования форм и отношений, сходных с формами и отношениями в обычном пространстве.
В качестве примера абстрактной геометрической теории можно рассмотреть Г. n-мерного евклидова пространства. Она строится путём простого обобщения основных положений обычной Г., причём для этого имеется несколько возможностей: можно, например, обобщать аксиомы обычной Г., но можно исходить и из задания точек координатами. При втором подходе n-мерное пространство определяют как множество каких-либо элементов-точек, задаваемых (каждая) n числами x1, x2,¼, xn, расположенными в определённом порядке, — координатами точек. Далее, расстояние между точками Х = (x1, x2,¼, xn) и X'= (x’1, x’2,¼, х’n) определяется формулой:
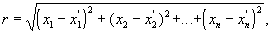
что является прямым обобщением известной формулы для расстояния в трёхмерном пространстве. Движение определяют как преобразование фигуры, которое не изменяет расстояний между её точками. Тогда предмет n-мерной Г. определяется как исследование тех свойств фигур, которые не меняются при движениях. На этой основе легко вводятся понятия о прямой, о плоскостях различного числа измерений от двух до n—1, о шаре и т.д. Т. о. складывается богатая содержанием теория, во многом аналогичная обычной евклидовой Г., но во многом и отличная от неё. Нередко бывает, что результаты, полученные для трёхмерного пространства, легко переносятся с соответствующими изменениями на пространство любого числа измерений. Например, теорема о том, что среди всех тел одинакового объёма наименьшую площадь поверхности имеет шар, читается дословно так же в пространстве любого числа измерений [нужно лишь иметь в виду n-мерный объём, (n—1)-мерную площадь и n-мерный шар, которые определяются вполне аналогично соответствующим понятиям обычной Г.]. Далее, в n-мерном пространстве объём призмы равен произведению площади основания на высоту, а объём пирамиды — такому произведению, деленному на n. Такие примеры можно продолжить. С др. стороны, в многомерных пространствах обнаруживаются также качественно новые факты.
Истолкования геометрии. Одна и та же геометрическая теория допускает разные приложения, разные истолкования (осуществления, модели, или интерпретации). Всякое приложение теории и есть не что иное, как осуществление некоторых её выводов в соответствующей области явлений.
Возможность разных осуществлений является общим свойством всякой математической теории. Так, арифметические соотношения реализуются на самых различных наборах предметов; одно и то же уравнение описывает часто совсем разные явления. Математика рассматривает лишь форму явления, отвлекаясь от содержания, а с точки зрения формы многие качественно различные явления оказываются часто сходными. Разнообразие приложений математики и, в частности, Г. обеспечивается именно её абстрактным характером. Считают, что некоторая система объектов (область явлений) даёт осуществление теории, если отношения в этой области объектов могут быть описаны на языке теории так, что каждое утверждение теории выражает тот или иной факт, имеющий место в рассматриваемой области. В частности, если теория строится на основе некоторой системы аксиом, то истолкование этой теории состоит в таком сопоставлении её понятий с некоторыми объектами и их отношениями, при котором аксиомы оказываются выполненными для этих объектов.
Евклидова Г. возникла как отражение фактов действительности. Её обычная интерпретация, в которой прямыми считаются натянутые нити, движением — механическое перемещение и т.д., предшествует Г. как математической теории. Вопрос о других интерпретациях не ставился и не мог быть поставлен, пока не выявилось более абстрактное понимание геометрии. Лобачевский создал неевклидову Г. как возможную геометрию, и тогда возник вопрос о её реальном истолковании. Эта задача была решена в 1868 Э. Бельтрами, который заметил, что геометрия Лобачевского совпадает с внутренней Г. поверхностей постоянной отрицательной кривизны, т. е. теоремы геометрии Лобачевского описывают геометрические факты на таких поверхностях (при этом роль прямых выполняют геодезические линии, а роль движений — изгибания поверхности на себя). Поскольку вместе с тем такая поверхность есть объект евклидовой Г., оказалось, что геометрия Лобачевского истолковывается в понятиях геометрии Евклида. Тем самым была доказана непротиворечивость геометрии Лобачевского, т.к. противоречие в ней в силу указанного истолкования влекло бы противоречие в геометрии Евклида.
Т. о., выясняется двоякое значение истолкования геометрической теории — физическое и математическое. Если речь идёт об истолковании на конкретных объектах, то получается опытное доказательство истинности теории (конечно, с соответствующей точностью); если же сами объекты имеют абстрактный характер (как геометрическая поверхность в рамках геометрии Евклида), то теория связывается с другой математической теорией, в данном случае с евклидовой Г., а через неё с суммированными в ней опытными данными. Такое истолкование одной математической теории посредством другой стало математическим методом обоснования новых теорий, приёмом доказательства их непротиворечивости, поскольку противоречие в новой теории порождало бы противоречие в той теории, в которой она интерпретируется. Но теория, посредством которой производится истолкование, в свою очередь, нуждается в обосновании. Поэтому указанный математический метод не снимает того, что окончательным критерием истины для математических теорий остаётся практика. В настоящее время геометрические теории чаще всего истолковывают аналитически; например, точки на плоскости Лобачевского можно связывать с парами чисел х и у, прямые — определять уравнениями и т.п. Этот приём даёт обоснование теории потому, что сам математический анализ обоснован, в конечном счёте, огромной практикой его применения.
Современная геометрия. Принятое в современной математике формально-математическое определение понятий пространства и фигуры исходит из понятия множества (см. Множеств теория). Пространство определяется как множество каких-либо элементов («точек») с условием, что в этом множестве установлены некоторые отношения, сходные с обычными пространственными отношениями. Множество цветов, множество состояний физической системы, множество непрерывных функций, заданных на отрезке [0, 1], и т.п. образуют пространства, где точками будут цвета, состояния, функции. Точнее, эти множества понимаются как пространства, если в них фиксируются только соответствующие отношения, например расстояние между точками, и те свойства и отношения, которые через них определяются. Так, расстояние между функциями можно определить как максимум абсолютной величины их разности: max|f (x)—g (x)|. Фигура определяется как произвольное множество точек в данном пространстве. (Иногда пространство — это система из множеств элементов. Например, в проективной Г. принято рассматривать точки, прямые и плоскости как равноправные исходные геометрические объекты, связанные отношениями «соединения».)
Основные типы отношений, которые в разных комбинациях приводят ко всему разнообразию «пространств» современной Г., следующие:
1) Общими отношениями, имеющимися во всяком множестве, являются отношения принадлежности и включения: точка принадлежит множеству, и одно множество есть часть другого. Если приняты во внимание только эти отношения, то в множестве не определяется ещё никакой «геометрии», оно не становится пространством. Однако, если выделены некоторые специальные фигуры (множества точек), то «геометрия» пространства может определяться законами связи точек с этими фигурами. Такую роль играют аксиомы сочетания в элементарной, аффинной, проективной Г.; здесь специальными множествами служат прямые и плоскости.
Тот же принцип выделения некоторых специальных множеств позволяет определить понятие топологического пространства — пространства, в котором в качестве специальных множеств выделены «окрестности» точек (с условием, что точка принадлежит своей окрестности и каждая точка имеет хотя бы одну окрестность; наложение на окрестности дальнейших требований определяет тот или иной тип топологических пространств). Если всякая окрестность заданной точки имеет общие точки с некоторым множеством, то такая точка называется точкой прикосновения этого множества. Два множества можно назвать соприкасающимися, если хотя бы одно из них содержит точки прикосновения другого; пространство или фигура будет непрерывной, или, как говорят, связной, если её нельзя разбить на две несоприкасающиеся части; преобразование непрерывно, если оно не нарушает соприкосновений. Т. о., понятие топологического пространства служит для математического выражения понятия непрерывности. [Топологическое пространство можно определить также другими специальными множествами (замкнутыми, открытыми) или непосредственно отношением прикосновения, при котором любому множеству точек ставятся в соответствие его точки прикосновения.] Топологические пространства как таковые, множества в них и их преобразования служат предметом топологии. Предмет собственно Г. (в значительной её части) составляет исследование топологических пространств и фигур в них, наделённых ещё дополнительными свойствами.
2) Второй важнейший принцип определения тех или иных пространств и их исследования представляет введение координат. Многообразием называется такое (связное) топологическое пространство, в окрестности каждой точки которого можно ввести координаты, поставив точки окрестности во взаимно однозначное и взаимно непрерывное соответствие с системами из n действительных чисел x1, x2,(, xn. Число n есть число измерений многообразия. Пространства, изучаемые в большинстве геометрических теорий, являются многообразиями; простейшие геометрические фигуры (отрезки, части поверхностей, ограниченные кривыми, и т.п.) обычно — куски многообразий. Если среди всех систем координат, которые можно ввести в кусках многообразия, выделяются системы координат такого рода, что одни координаты выражаются через другие дифференцируемыми (то или иное число раз) или аналитическими функциями, то получают т. н. гладкое (аналитическое) многообразие. Это понятие обобщает наглядное представление о гладкой поверхности. Гладкие многообразия как таковые составляют предмет т. н. дифференциальной топологии. В собственно Г. они наделяются дополнительными свойствами. Координаты с принятым условием дифференцируемости их преобразований дают почву для широкого применения аналитических методов — дифференциального и интегрального исчисления, а также векторного и тензорного анализа (см. Векторное исчисление, Тензорное исчисление). Совокупность теорий Г., развиваемых этими методами, образует общую дифференциальную Г.; простейшим случаем её служит классическая теория гладких кривых и поверхностей, которые представляют собою не что иное, как одно- и двумерные дифференцируемые многообразия.
3) Обобщение понятия движения как преобразования одной фигуры в другую приводит к общему принципу определения разных пространств, когда пространством считается множество элементов (точек), в котором задана группа взаимно однозначных преобразований этого множества на себя. «Геометрия» такого пространства состоит в изучении тех свойств фигур, которые сохраняются при преобразованиях из этой группы. Поэтому с точки зрения такой Г. фигуры можно считать «равными», если одна переходит в другую посредством преобразования из данной группы. Например, евклидова Г. изучает свойства фигур, сохраняющиеся при движениях, аффинная Г. — свойства фигур, сохраняющиеся при аффинных преобразованиях, топология — свойства фигур, сохраняющиеся при любых взаимно однозначных и непрерывных преобразованиях. В эту же схему включаются геометрия Лобачевского, проективная Г. и др. Фактически этот принцип соединяется с введением координат. Пространство определяется как гладкое многообразие, в котором преобразования задаются функциями, связывающими координаты каждой данной точки и той, в которую она переходит (координаты образа точки задаются как функции координат самой точки и параметров, от которых зависит преобразование; например, аффинные преобразования определяются как линейные: x'i = ai1x1 + ai2x2 +¼+ ainxn, i = 1, ¼, n). Поэтому общим аппаратом разработки таких «геометрий» служит теория непрерывных групп преобразований. Возможна другая, по существу эквивалентная, точка зрения, согласно которой задаются не преобразования пространства, а преобразования координат в нём, причём изучаются те свойства фигур, которые одинаково выражаются в разных системах координат. Эта точка зрения нашла применение в теории относительности, которая требует одинакового выражения физических законов в разных системах координат, называемых в физике системами отсчёта.
4) Другой общий принцип определения пространств, указанный в 1854 Риманом, исходит из обобщения понятия о расстоянии. По Риману, пространство — это гладкое многообразие, в котором задан закон измерения расстояний, точнее длин, бесконечно малыми шагами, т. е. задаётся дифференциал длины дуги кривой как функция координат точки кривой и их дифференциалов. Это есть обобщение внутренней Г. поверхностей, определённой Гауссом как учение о свойствах поверхностей, которые могут быть установлены измерением длин кривых на ней. Простейший случай представляют т. н. римановы пространства, в которых в бесконечно малом имеет место теорема Пифагора (т. е. в окрестности каждой точки можно ввести координаты так, что в этой точке квадрат дифференциала длины дуги будет равен сумме квадратов дифференциалов координат; в произвольных же координатах он выражается общей положительной квадратичной формой; см. Римановы геометрии). Такое пространство, следовательно, евклидово в бесконечно малом, но в целом оно может не быть евклидовым, подобно тому как кривая поверхность лишь в бесконечно малом может быть сведена к плоскости с соответствующей точностью. Геометрии Евклида и Лобачевского оказываются частным случаем этой римановой Г. Наиболее широкое обобщение понятия расстояния привело к понятию общего метрического пространства как такого множества элементов, в котором задана «метрика», т. е. каждой паре элементов отнесено число — расстояние между ними, подчинённое только очень общим условиям. Эта идея играет важную роль в функциональном анализе и лежит в основе некоторых новейших геометрических теорий, таких, как внутренняя Г. негладких поверхностей и соответствующие обобщения римановой Г.
5) Соединение идеи Римана об определении «геометрии» в бесконечно малых областях многообразия с определением «геометрии» посредством группы преобразований привело (Э. Картан, 1922—25) к понятию о таком пространстве, в котором преобразования задаются лишь в бесконечно малых областях; иными словами, здесь преобразования устанавливают связь только бесконечно близких кусков многообразия: один кусок преобразуется в другой, бесконечно близкий. Поэтому говорят о пространствах со «связностью» того или иного типа. В частности, пространства с «евклидовой связностью» суть римановы. Дальнейшие обобщения восходят к понятию о пространстве как о гладком многообразии, на котором задано вообще «поле» какого-либо «объекта», которым может служить квадратичная форма, как в римановой Г., совокупность величин, определяющих связность, тот или иной тензор и др. Сюда же можно отнести введённые в недавнее время т. н. расслоенные пространства. Эти концепции включают, в частности, связанное с теорией относительности обобщение римановой Г., когда рассматриваются пространства, где метрика задаётся уже не положительной, а знакопеременной квадратичной формой (такие пространства также называют римановыми, или псевдоримановыми, если хотят отличить их от римановых в первоначальном смысле). Эти пространства являются пространствами со связностью, определённой соответствующей группой, отличной от группы евклидовых движений.
На почве теории относительности возникла теория пространств, в которых определено понятие следования точек, так что каждой точке Х отвечает множество V (X) следующих за нею точек. (Это является естественным математическим обобщением следования событий, определённого тем, что событие Y следует за событием X, если Х воздействует на Y, и тогда Y следует за Х во времени в любой системе отсчёта.) Т. к. само задание множеств V определяет точки, следующие за X, как принадлежащие множеству V (X), то определение этого типа пространств оказывается применением первого из перечисленных выше принципов, когда «геометрия» пространства определяется выделением специальных множеств. Конечно, при этом множества V должны быть подчинены соответствующим условиям; в простейшем случае — это выпуклые конусы. Эта теория включает теорию соответствующих псевдоримановых пространств.
6) Аксиоматический метод в его чистом виде служит теперь либо для оформления уже готовых теорий, либо для определения общих типов пространств с выделенными специальными множествами. Если же тот или иной тип более конкретных пространств определяют, формулируя их свойства как аксиомы, то используют либо координаты, либо метрику и др. Непротиворечивость и тем самым осмысленность аксиоматической теории проверяется указанием модели, на которой она реализуется, как это впервые было сделано для геометрии Лобачевского. Сама модель строится из абстрактных математических объектов, поэтому «окончательное обоснование» любой геометрической теории уходит в область оснований математики вообще, которые не могут быть окончательными в полном смысле, но требуют углубления (см. Математика, Аксиоматический метод).
Перечисленные принципы в разных сочетаниях и вариациях порождают обширное разнообразие геометрических теорий. Значение каждой из них и степень внимания к её задачам определяются содержательностью этих задач и получаемых результатов, её связями с др. теориями Г., с др. областями математики, с точным естествознанием и задачами техники. Каждая данная геометрическая теория определяется среди других геометрических теорий, во-первых, тем, какое пространство или какого типа пространства в ней рассматриваются. Во-вторых, в определение теории входит указание на исследуемые фигуры. Так различают теории многогранников, кривых, поверхностей, выпуклых тел и т.д. Каждая из этих теорий может развиваться в том или ином пространстве. Например, можно рассматривать теорию многогранников в обычном евклидовом пространстве, в n-мерном евклидовом пространстве, в пространстве Лобачевского и др. Можно развивать обычную теорию поверхностей, проективную, в пространстве Лобачевского и т.д. В-третьих, имеет значение характер рассматриваемых свойств фигур. Так, можно изучать свойства поверхностей, сохраняющиеся при тех или иных преобразованиях; можно различать учение о кривизне поверхностей, учение об изгибаниях (т. е. о деформациях, не меняющих длин кривых на поверхности), внутреннюю Г. Наконец, в определение теории можно включать её основной метод и характер постановки задач. Так различают Г.: элементарную, аналитическую, дифференциальную; например, можно говорить об элементарной или аналитической Г. пространства Лобачевского. Различают Г. «в малом», рассматривающую лишь свойства сколь угодно малых кусков геометрического образа (кривой, поверхности, многообразия), от Г. «в целом», изучающей, как ясно из её названия, геометрические образы в целом на всём их протяжении. Очень общим является различение аналитических методов и методов синтетической Г. (или собственно геометрических методов); первые используют средства соответствующих исчислений: дифференциального, тензорного и др., вторые оперируют непосредственно геометрическими образами.
Из всего разнообразия геометрических теорий фактически более всего развиваются n-мерная евклидова Г. и риманова (включая псевдориманову) Г. В первой разрабатывается, в особенности, теория кривых и поверхностей (и гиперповерхностей разного числа измерений), причём особое развитие получает исследование поверхностей «в целом» и поверхностей, существенно более общих, чем гладкие, изучавшиеся в классической дифференциальной Г.; сюда же включаются многогранники (многогранные поверхности). Затем нужно назвать теорию выпуклых тел, которая, впрочем, в большой части может быть отнесена к теории поверхностей в целом, т.к. тело определяется своей поверхностью. Далее — теория правильных систем фигур, т. е. допускающих движения, переводящие всю систему саму в себя и какую-либо её фигуру в любую другую (см. Федоровские группы). Можно отметить, что значительное число важнейших результатов в этих областях принадлежат сов. геометрам: очень полная разработка теории выпуклых поверхностей и существенное развитие теории общих невыпуклых поверхностей, разнообразные теоремы о поверхностях в целом (существования и единственности выпуклых поверхностей с заданной внутренней метрикой или с заданной той пли иной «функцией кривизны», теорема о невозможности существования полной поверхности с кривизной, всюду меньшей какого-либо отрицательного числа, и др.), исследование правильного деления пространства и др.
В теории римановых пространств исследуются вопросы, касающиеся связи их метрических свойств с топологическим строением, поведение геодезических (кратчайших на малых участках) линий в целом, как, например, вопрос о существовании замкнутых геодезических, вопросы «погружения», т. е. реализации данного n-мерного риманова пространства в виде n-мерной поверхности в евклидовом пространстве какого-либо числа измерений, вопросы псевдоримановой Г., связанные с общей теорией относительности, и др. К этому можно добавить развитие разнообразных обобщений римановой Г. как в духе общей дифференциальной Г., так и в духе обобщений синтетической Г.
В дополнение следует упомянуть алгебраическую геометрию, развившуюся из аналитической Г. и исследующую прежде всего геометрические образы, задаваемые алгебраическими уравнениями; она занимает особое место, т.к. включает не только геометрические, но также алгебраические и арифметические проблемы. Существует также обширная и важная область исследования бесконечномерных пространств, которая, однако, не причисляется к Г., а включается в функциональный анализ, т.к. бесконечномерные пространства конкретно определяются как пространства, точками которых служат те или иные функции. Тем не менее в этой области есть много результатов и проблем, носящих подлинно геометрический характер и которые поэтому следует относить к Г.
Значение геометрии. Применение евклидовой Г. представляет самое обычное явление всюду, где определяются площади, объёмы и т.п. Вся техника, поскольку в ней играют роль формы и размеры тел, пользуется евклидовой Г. Картография, геодезия, астрономия, все графические методы, механика немыслимы без Г. Ярким примером является открытие И. Кеплером факта вращения планет по эллипсам; он мог воспользоваться тем, что эллипс был изучен ещё древними геометрами. Глубокое применение Г. представляет геометрическая кристаллография, послужившая источником и областью приложения теории правильных систем фигур (см. Кристаллография).
Более отвлечённые геометрические теории находят широкое применение в механике и физике, когда совокупность состояний какой-либо системы рассматривается как некоторое пространство (см. раздел Обобщение предмета геометрии). Так, все возможные конфигурации (взаимное расположение элементов) механической системы образуют «конфигурационное пространство»; движение системы изображается движением точки в этом пространстве. Совокупность всех состояний физической системы (в простейшем случае — положения и скорости образующих систему материальных точек, например молекул газа) рассматривается как «фазовое пространство» системы. Эта точка зрения находит, в частности, применение в статистической физике и др.
Впервые понятие о многомерном пространстве зародилось в связи с механикой ещё у Ж. Лагранжа, когда к трём пространств. координатам х, у, z в качестве четвёртой формально присоединяется время t. Так появляется четырёхмерное «пространство — время», где точка определяется четырьмя координатами х, у, z, t. Каждое событие характеризуется этими четырьмя координатами и, отвлеченно, множество всех событий в мире оказывается четырёхмерным пространством. Этот взгляд получил развитие в геометрической трактовке теории относительности, данной Г. Минковским, а потом в построении А. Эйнштейном общей теории относительности. В ней он воспользовался четырехмерной римановой (псевдоримановой) Г. Так геометрические теории, развившиеся из обобщения данных пространственного опыта, оказались математическим методом построения более глубокой теории пространства и времени. В свою очередь теория относительности дала мощный толчок развитию общих геометрических теорий. Возникнув из элементарной практики, Г. через ряд абстракций и обобщений возвращается к естествознанию и практике на более высокой ступени в качестве метода.
С геометрической точки зрения многообразие пространства — времени обычно трактуется в общей теории относительности как неоднородное римановского типа, но с метрикой, определяемой знакопеременной формой, приводимой в бесконечно малой области к виду
dx2 + dy2 + dz2 — c2dt2
(с — скорость света в вакууме). Само пространство, поскольку его можно отделить от времени, оказывается также неоднородным римановым. С современной геометрической точки зрения лучше смотреть на теорию относительности следующим образом. Специальная теория относительности утверждает, что многообразие пространства — времени есть псевдоевклидово пространство, т. е. такое, в котором роль «движений» играют преобразования, сохраняющие квадратичную форму
x2 + y2 + z2 — c2t2
точнее, это есть пространство с группой преобразований, сохраняющих указанную квадратичную форму. От всякой формулы, выражающей физический закон, требуется, чтобы она не менялась при преобразованиях группы этого пространства, которые суть так называемые преобразования Лоренца. Согласно же общей теории относительности, многообразие пространства — времени неоднородно и лишь в каждой «бесконечно малой» области сводится к псевдоевклидову, т. е. оно есть пространство картановского типа (см. раздел Современная геометрия). Однако такое понимание стало возможно лишь позже, т.к. само понятие о пространствах такого типа появилось после теории относительности и было развито под её прямым влиянием.
В самой математике положение и роль Г. определяются прежде всего тем, что через неё в математику вводилась непрерывность. Математика как наука о формах действительности сталкивается прежде всего с двумя общими формами: дискретностью и непрерывностью. Счёт отдельных (дискретных) предметов даёт арифметику, пространств. непрерывность изучает Г. Одним из основных противоречий, движущих развитие математики, является столкновение дискретного и непрерывного. Уже деление непрерывных величин на части и измерение представляют сопоставление дискретного и непрерывного: например, масштаб откладывается вдоль измеряемого отрезка отдельными шагами. Противоречие выявилось с. особой ясностью, когда в Древней Греции (вероятно, в 5 в. до н. э.) была открыта несоизмеримость стороны и диагонали квадрата: длина диагонали квадрата со стороной 1 не выражалась никаким числом, т.к. понятия иррационального числа не существовало. Потребовалось обобщение понятия числа — создание понятия иррационального числа (что было сделано лишь много позже в Индии). Общая же теория иррациональных чисел была создана лишь в 70-х гг. 19 в. Прямая (а вместе с нею и всякая фигура) стала рассматриваться как множество точек. Теперь эта точка зрения является господствующей. Однако затруднения теории множеств показали её ограниченность. Противоречие дискретного и непрерывного не может быть полностью снято.
Общая роль Г. в математике состоит также в том, что с нею связано идущее от пространственных представлений точное синтетическое мышление, часто позволяющее охватить в целом то, что достигается анализом и выкладками лишь через длинную цепь шагов. Так, Г. характеризуется не только своим предметом, но и методом, идущим от наглядных представлений и оказывающимся плодотворным в решении многих проблем др. областей математики. В свою очередь, Г. широко использует их методы. Т. о., одна и та же математическая проблема может сплошь и рядом трактоваться либо аналитически, либо геометрически, или в соединении обоих методов.
В известном смысле, почти всю математику можно рассматривать как развивающуюся из взаимодействия алгебры (первоначально арифметики) и Г., а в смысле метода — из сочетания выкладок и геометрических представлений. Это видно уже в понятии совокупности всех вещественных чисел как числовой прямой, соединяющей арифметические свойства чисел с непрерывностью. Вот некоторые основные моменты влияния Г. в математике.
1) В возникновении и развитии анализа Г. наряду с механикой имела решающее значение. Интегрирование происходит от нахождения площадей и объемов, начатого ещё древними учёными, причём площадь и объём как величины считались определёнными; никакое аналитическое определение интеграла не давалось до 1-й половины 19 в. Проведение касательных было одной из задач, породивших дифференцирование. Графическое представление функций сыграло важную роль в выработке понятий анализа и сохраняет своё значение. В самой терминологии анализа виден геометрический источник его понятий, как, например, в терминах: «точка разрыва», «область изменения переменной» и т.п. Первый курс анализа, написанный в 1696 Г. Лопиталем, назывался: «Анализ бесконечно малых для понимания кривых линий». Теория дифференциальных уравнений в большей части трактуется геометрически (интегральные кривые и т.п.). Вариационное исчисление возникло и развивается в большой мере на задачах Г., и её понятия играют в нём важную роль.
2) Комплексные числа окончательно утвердились в математике на рубеже 18—19 вв. только вследствие сопоставления их с точками плоскости, т. е. путём построения «комплексной плоскости». В теории функций комплексного переменного геометрическими методам отводится существенная роль. Само понятие аналитической функции w = f (z) комплексного переменного может быть определено чисто геометрически: такая функция есть конформное отображение плоскости z (или области плоскости z) в плоскость w. Понятия и методы римановой Г. находят применение в теории функций нескольких комплексных переменных.
3) Основная идея функционального анализа состоит в том, что функции данного класса (например, все непрерывные функции, заданные на отрезке [0,1]) рассматриваются как точки «функционального пространства», причём отношения между функциями истолковываются как геометрические отношения между соответствующими точками (например, сходимость функций истолковывается как сходимость точек, максимум абсолютной величины разности функций — как расстояние, и т.п.). Тогда многие вопросы анализа получают геометрическое освещение, оказывающееся во многих случаях очень плодотворным. Вообще, представление тех или иных математических объектов (функций, фигур и др.) как точек некоторого пространства с соответствующим геометрическим толкованием отношений этих объектов является одной из наиболее общих и плодотворных идей современной математики, проникшей почти во все её разделы.
4) Г. оказывает влияние на алгебру и даже на арифметику — теорию чисел. В алгебре используют, например, понятие векторного пространства. В теории чисел создано геометрическое направление, позволяющее решать многие задачи, едва поддающиеся вычислительному методу. В свою очередь нужно отметить также графические методы расчётов (см. Номография) и геометрические методы современной теории вычислений и вычислительных машин.
5) Логическое усовершенствование и анализ аксиоматики Г. играли определяющую роль в выработке абстрактной формы аксиоматического метода с его полным отвлечением от природы объектов и отношений, фигурирующих в аксиоматизируемой теории. На том же материале вырабатывались понятия непротиворечивости, полноты и независимости аксиом.
В целом взаимопроникновение Г. и др. областей математики столь тесно, что часто границы оказываются условными и связанными лишь с традицией. Почти или вовсе не связанными с Г. остаются лишь такие разделы, как абстрактная алгебра, математическая логика и некоторые др.
Лит.: Основные классические работы. Евклид, Начала, пер. с греч., кн. 1—15, М. — Л.,1948—50; Декарт Р., Геометрия, пер. с латин., М. — Л., 1938; Монж Г., Приложения анализа к геометрии, пер. с франц., М. — Л., 1936; Ponselet J. V., Traite des proprietes projectives des figures, Metz — Р., 1822; Гаусс К. Ф., Общие исследования о кривых поверхностях, пер. с нем., в сборнике: Об основаниях геометрии, М., 1956; Лобачевский Н. И., Полн. собр. соч., т. 1—3, М. — Л., 1946—51; Больаи Я., Appendix. Приложение,..., пер. с латин., М. — Л., 1950; Риман Б., О гипотезах, лежащих в основаниях геометрии, пер. с нем., в сборнике: Об основаниях геометрии, М., 1956; Клейн Ф., Сравнительное обозрение новейших геометрических исследований («Эрлангенская программа»), там же; Картан Э., Группы голономии обобщенных пространств, пер. с франц., в кн.: VIII-й Международный конкурс на соискание премии имени Николая Ивановича Лобачевского (1937 год), Казань, 1940; Гильберт Д., Основания геометрии, пер. с нем., М. — Л., 1948.
История. Кольман Э., История математики в древности, М., 1961; Юшкевич А. П., История математики в средние века, М., 1961; Вилейтнер Г., История математики от Декарта до середины 19 столетия, пер. с нем., 2 изд., М., 1966; Cantor М., Vorlesungen über die Geschichte der Mathematik, Bd 1—4, Lpz., 1907—08.
Курсы. а) Основания геометрии. Каган В. Ф., Основания геометрии, ч. 1, М. — Л., 1949; Ефимов Н. В., Высшая геометрия, 4 изд., М., 1961; Погорелов А. В., Основания геометрии, 3 изд., М., 1968.
б) Элементарная геометрия. Адамар Ж., Элементарная геометрия, пер. с франц., ч. 1, 3 изд., М., 1948, ч. 2, М., 1938; Погорелов А. В., Элементарная геометрия, М., 1969.
в) Аналитическая геометрия. Александров П. С., Лекции по аналитической геометрии..., М., 1968; Погорелов А. В., Аналитическая геометрия, 3 изд., М., 1968.
г) Дифференциальная геометрия. Рашевский П. К., Курс дифференциальной геометрии, 3 изд., М. — Л., 1950; Каган В. Ф., Основы теории поверхностей в тензорном изложении, ч. 1—2, М. — Л., 1947—48; Погорелов А. В., Дифференциальная геометрия, М., 1969.
д) Начертательная и проективная геометрия. Глаголев Н. А., Начертательная геометрия, 3 изд., М. — Л., 1953; Ефимов Н. В., Высшая геометрия, 4 изд., М., 1961.
е) Риманова геометрия и её обобщения. Рашевский П. К., Риманова геометрия и тензорный анализ, 2 изд., М. — Л., 1964; Норден А. П., Пространства аффинной связности, М. — Л., 1950; Картан Э., Геометрия римановых пространств, пер. с франц., М. — Л., 1936; Эйзенхарт Л. П., Риманова геометрия, пер. с англ., М., 1948.
Некоторые монографии по геометрии. Федоров Е. С., Симметрия и структура кристаллов. Основные работы, М., 1949; Александров А. Д., Выпуклые многогранники, М. — Л., 1950; его же, Внутренняя геометрия выпуклых поверхностей, М. — Л., 1948; Погорелов А. В., Внешняя геометрия выпуклых поверхностей, М., 1969; Буземан Г., Геометрия геодезических, пер. с англ., М., 1962; его же, Выпуклые поверхности, пер. с англ., М., 1964; Картан Э., Метод подвижного репера, теория непрерывных групп и обобщенные пространства, пер. с франц., М. — Л., 1936; Фиников С. П., Метод внешних форм Картана в дифференциальной геометрии, М. — Л., 1948; его же, Проективно-дифференциальная геометрия, М. — Л., 1937; его же, Теория конгруенций, М. — Л., 1950; Схоутен И. А., Стройк Д. Дж., Введение в новые методы дифференциальной геометрии, пер. с англ., т. 1—2, М. — Л., 1939—48; Номидзу К., Группы Ли и дифференциальная геометрия, пер. с англ., М., 1960; Милнор Дж., Теория Морса, пер. с англ., М., 1965.
А. Д. Александров.