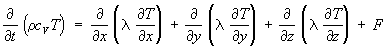Теплопроводности уравнение, дифференциальное уравнение с частными производными параболического типа, описывающее процесс распространения теплоты в сплошной среде (газе, жидкости или твёрдом теле); основное уравнение математической теории теплопроводности. Т. у. выражает тепловой баланс для малого элемента объёма среды с учётом поступления теплоты от источников и тепловых потерь через поверхность элементарного объёма вследствие теплопроводности. Для изотропной неоднородной среды Т. у. имеет вид:

  ,

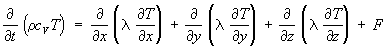где r — плотность среды; c_v — теплоёмкость среды при постоянном объёме; t — время; х, у, z — координаты; Т = Т (х, у, z, t) — температура, которая вычисляется при помощи Т. у.; l — коэффициент теплопроводности; F = F (x, y, z, t) — заданная плотность тепловых источников. Величины r, C_v, l зависят от координат и, вообще говоря, от температуры. Для анизотропной среды Т. у. вместо l содержит тензор теплопроводности l_ir, где i, k = 1, 2, 3.

  В случае изотропной однородной среды Т. у. принимает вид:

  ,

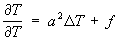где DT — Лапласа оператор, a² = l/(rc_v) — коэффициент температуропроводности; f = F/(rc_v). В стационарном состоянии, когда температура не меняется со временем, Т. у. переходит в Пуассона уравнение DТ = f/a² = F/l или, при отсутствии источников теплоты, в Лапласа уравнение DТ = 0. Основными задачами для Т. у. является Коши задача и смешанная краевая задача (см. Краевые задачи).

  Первые исследования Т. у. принадлежат Ж. Фурье (1822) и С. Пуассону (1835). Важные результаты в исследовании Т. у. были получены И. Г. Петровским, А. Н. Тихоновым, С. Л. Соболевым.

  Лит.: Карслоу Г. С., Теория теплопроводности, пер. с англ., М.— Л., 1947: Владимиров В. С., Уравнения математической физики, М., 1967; Тихонов А. Н., Самарский А. А., Уравнения математической физики, 3 изд., М., 1966.

  Д. Н. Зубарев.

Оглавление